岭(Ridge 线性回归大结局、 Lasso回归原理、公式推导)，你想要的这里都有( 五 ) _生活百科

文章插图
下面就是具体的生成过程：

首先先生成一个随机数据集

import numpy as npfrom matplotlib import pyplot as pltimport matplotlib as mplplt.style.use("ggplot")x1 = np.linspace(0, 20, 20)x2 = np.linspace(-10, 10, 20)y = .2 * x1 + .1 * x2# y 是 x1 和 x2的线性组合 所以我们最终线性回归要求的参数为 [0.2, 0.1]

x1:array([ 0.,1.05263158,2.10526316,3.15789474,4.21052632,5.26315789,6.31578947,7.36842105,8.42105263,9.47368421,10.52631579, 11.57894737, 12.63157895, 13.68421053, 14.73684211,15.78947368, 16.84210526, 17.89473684, 18.94736842, 20.])x2:array([-10.,-8.94736842,-7.89473684,-6.84210526,-5.78947368,-4.73684211,-3.68421053,-2.63157895,-1.57894737,-0.52631579,0.52631579,1.57894737,2.63157895,3.68421053,4.73684211,5.78947368,6.84210526,7.89473684,8.94736842,10.])

# 先将 x1 x2 进行拼接data = https://www.huyubaike.com/biancheng/np.vstack((x1, x2)).T

data:array([[0., -10.],[1.05263158,-8.94736842],[2.10526316,-7.89473684],[3.15789474,-6.84210526],[4.21052632,-5.78947368],[5.26315789,-4.73684211],[6.31578947,-3.68421053],[7.36842105,-2.63157895],[8.42105263,-1.57894737],[9.47368421,-0.52631579],[ 10.52631579,0.52631579],[ 11.57894737,1.57894737],[ 12.63157895,2.63157895],[ 13.68421053,3.68421053],[ 14.73684211,4.73684211],[ 15.78947368,5.78947368],[ 16.84210526,6.84210526],[ 17.89473684,7.89473684],[ 18.94736842,8.94736842],[ 20.,10.]])

x_max = 0.5points = 5000xx, yy = np.meshgrid(np.linspace(-x_max, x_max, points), np.linspace(-x_max, x_max, points))zz = np.zeros_like(xx)for i in range(points):for j in range(points):beta = np.array([xx[i][j], yy[i][j]]).Trss = ((data@beta - y) ** 2).sum()zz[i][j] = rssplt.contour(xx, yy, zz, levels=30, cmap=plt.cm.Accent, linewidths=1)sns.scatterplot(x=[0, 0.2], y=[0, 0.1], s=10)plt.text(x=0.2, y=0.1, s=r"$\hat{w}(0.2, 0.1)$", fontdict={"size":8})plt.text(x=0, y=0, s=r"$O(0, 0)$", fontdict={"size":8})plt.xlim(-.2,.5)plt.xlabel(r"$\hat{w}_1$")plt.ylabel(r"$\hat{w}_2$")plt.show()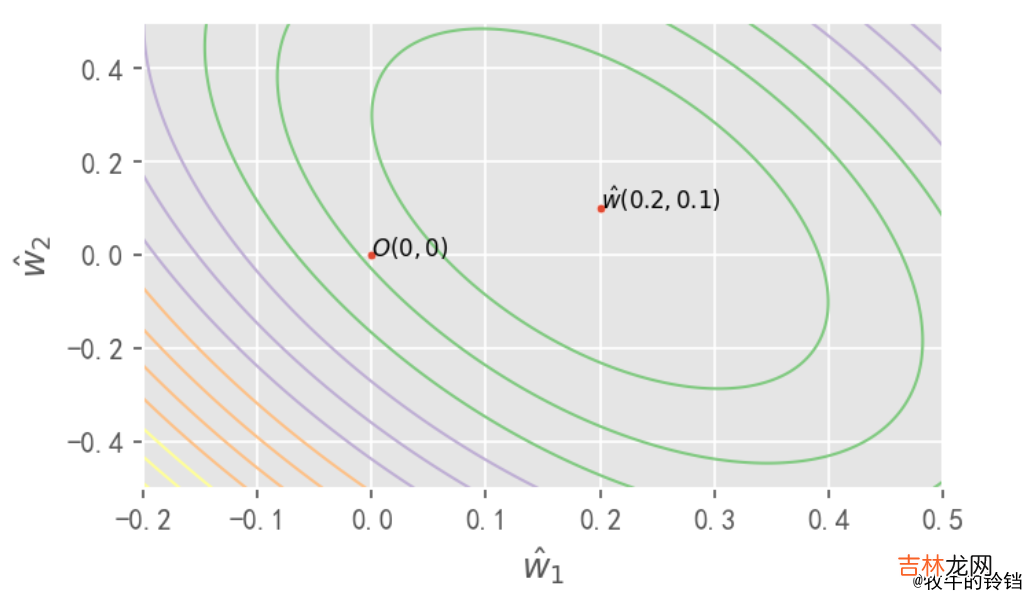

文章插图
我们最终需要求的 \(\hat{w}\) 是 \((0.2,0.1)\) 同时我们也计算了其他位置对应整个数据集的 \(RSS\) 。我么容易看出等高线都是以 \(\hat{w}(0.2, 0.1)\) 为圆心的椭圆，如果需要证明需要使用数学进行严格推到，这里我们只需要直到它的轨迹是一个椭圆即可，而我们知道
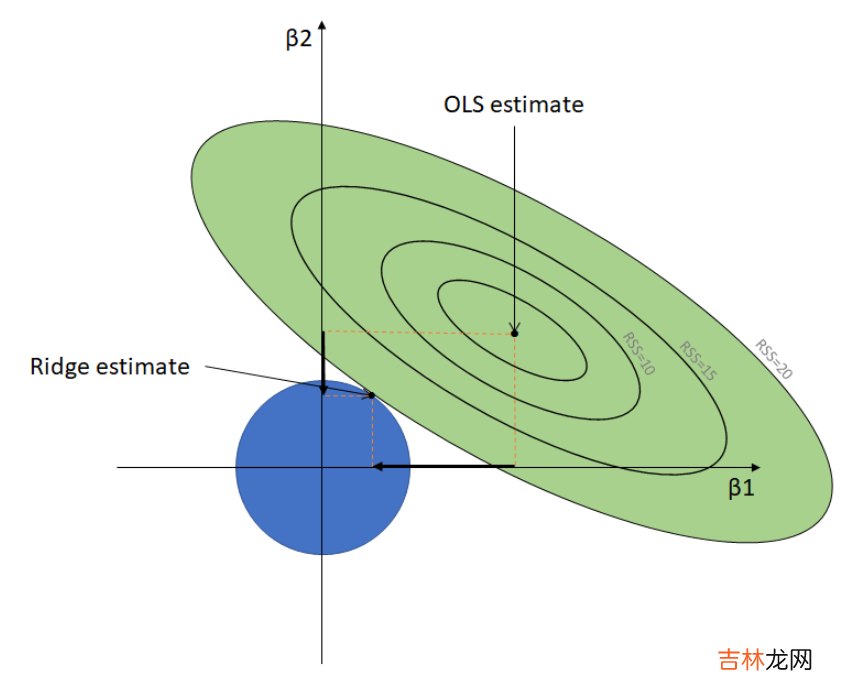
\[{\hat{w}_1^2} +{\hat{w}_1^2}\le C\]\(||\hat{w}||_2^2\) 的取值范围是一个圆，因为在岭回归损失函数的式子中有着两部分，它要同时满足这两个条件，那么他们两个曲线的交点就是 \(Ridge\) 的权重的取值，如下图所示：

文章插图
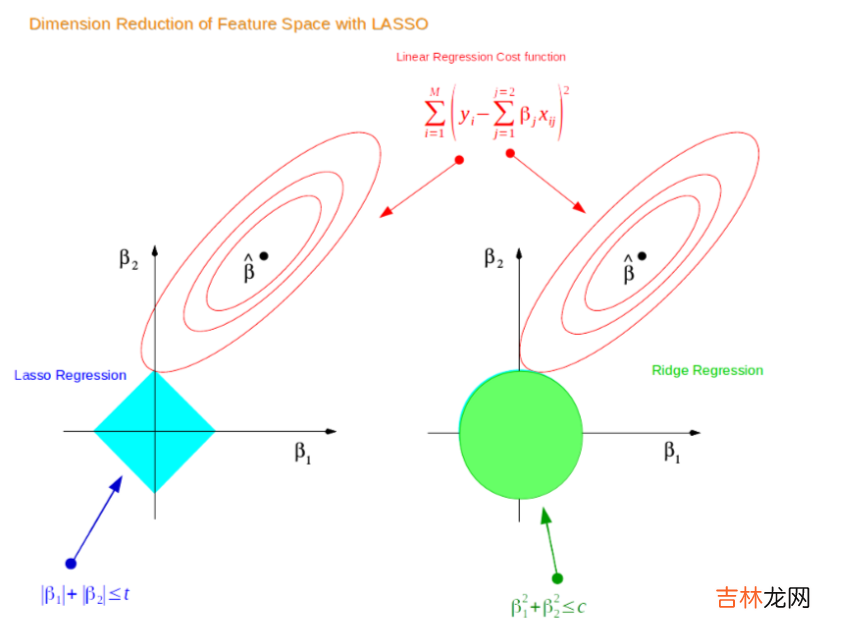
我们从上面的图很容易看出，最终两个权值的取值不会为0（如果为0他们的交点会在x或者y轴上），而是会随着权值的缩小而不断变小，即图中蓝色部分变小。同理我们也可以对 \(Lasso\) 回归最同样的事儿：

文章插图
从上图可以看出 \(Lasso\) 的权值是可以取到0的，注意是可以取到而不是一定取到，可以取到就说明，\(Lasso\) 回归可以在数据集有共线性的时候，对属性进行选择，即让某些属性对应的权值为0 。上面的结论都是在二维情况下产生的，可以推广到高维数据。以上就说明了在线性回归中 \(Ridge\) 和 \(Lasso\) 对权值的影响。
以上就是本篇文章的所有内容了，我是LeHung，我们下期再见！！！更多精彩内容合集可访问项目：https://github.com/Chang-LeHung/CSCore
关注公众号：一无是处的研究僧，了解更多计算机（Java、Python、计算机系统基础、算法与数据结构）知识。