2 。并且最下面一层的节点都集中在该层最左边的若干位置上 。2 个 。如上图中的树也是满二叉树 。邻接矩阵和邻接表的形式存储树 。3.1 邻接矩阵存储邻接矩阵是顺序表存储方案 。
3.1.1 思路流程
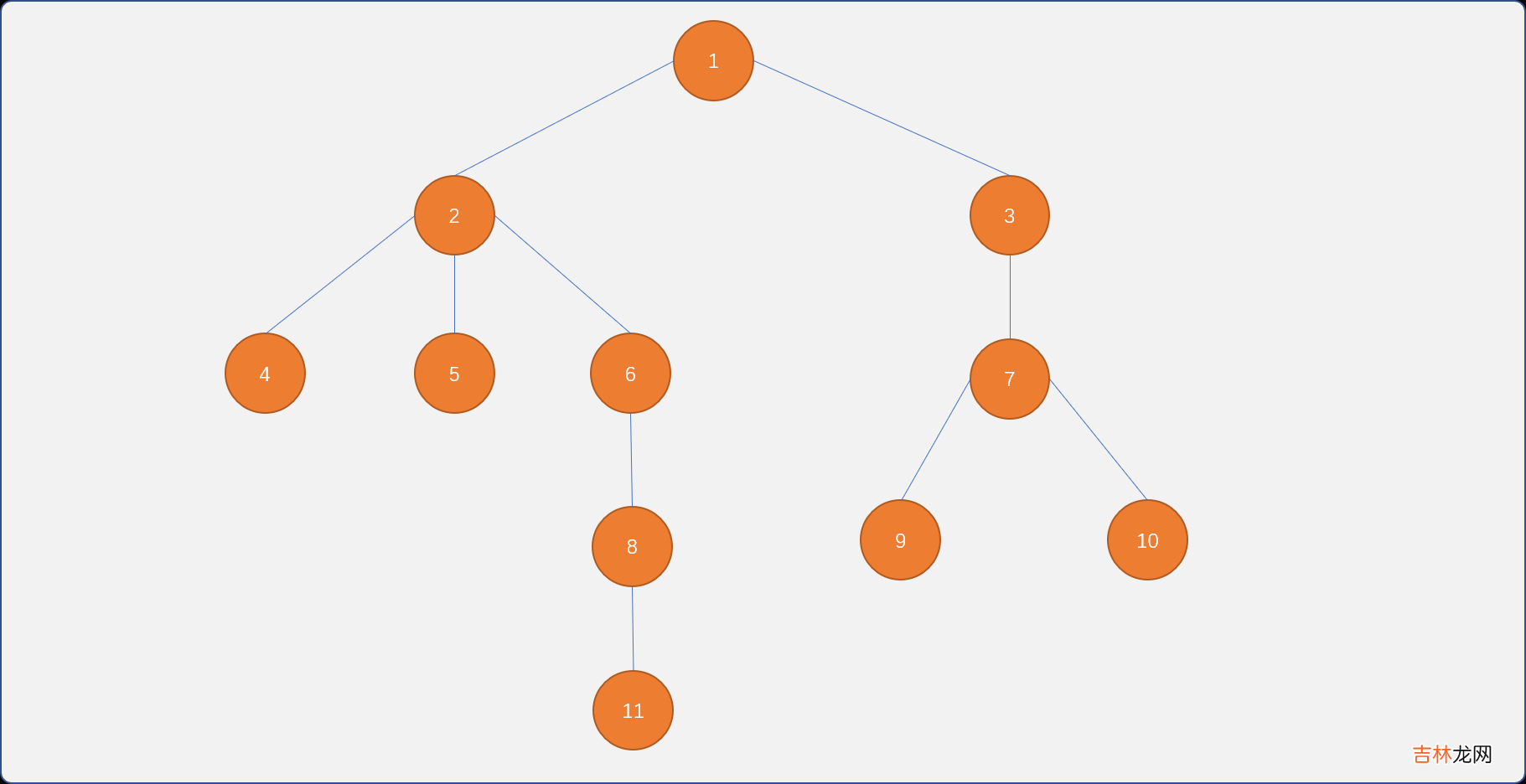
- 给树中的每一个节点从小到大进行编号 。如下图,树共有
11个节点 。
文章插图
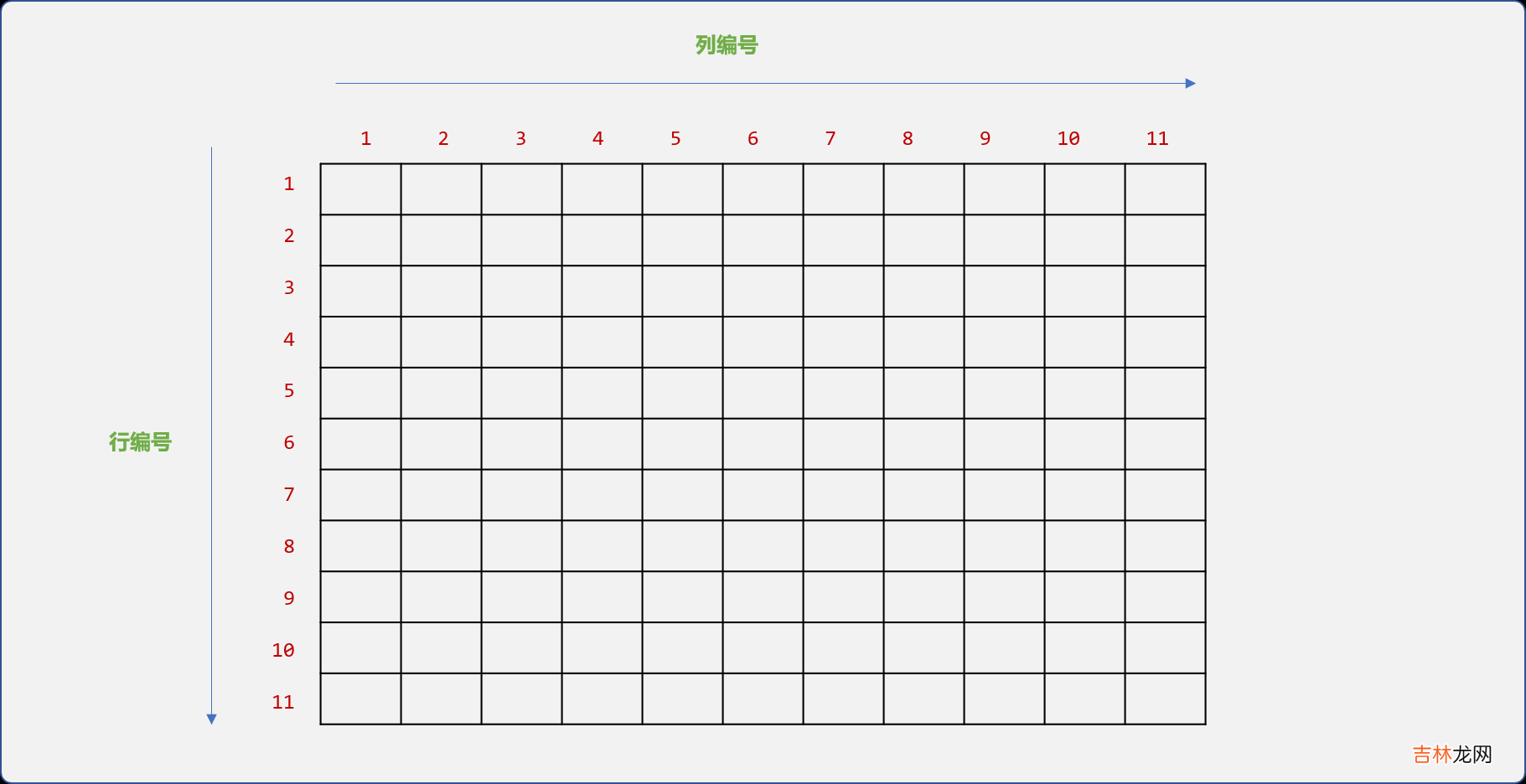
- 创建一个
11X11的名为arrTree的矩阵 ,行和列的编号对应节点的编号,并初始矩阵的值都为0。
文章插图
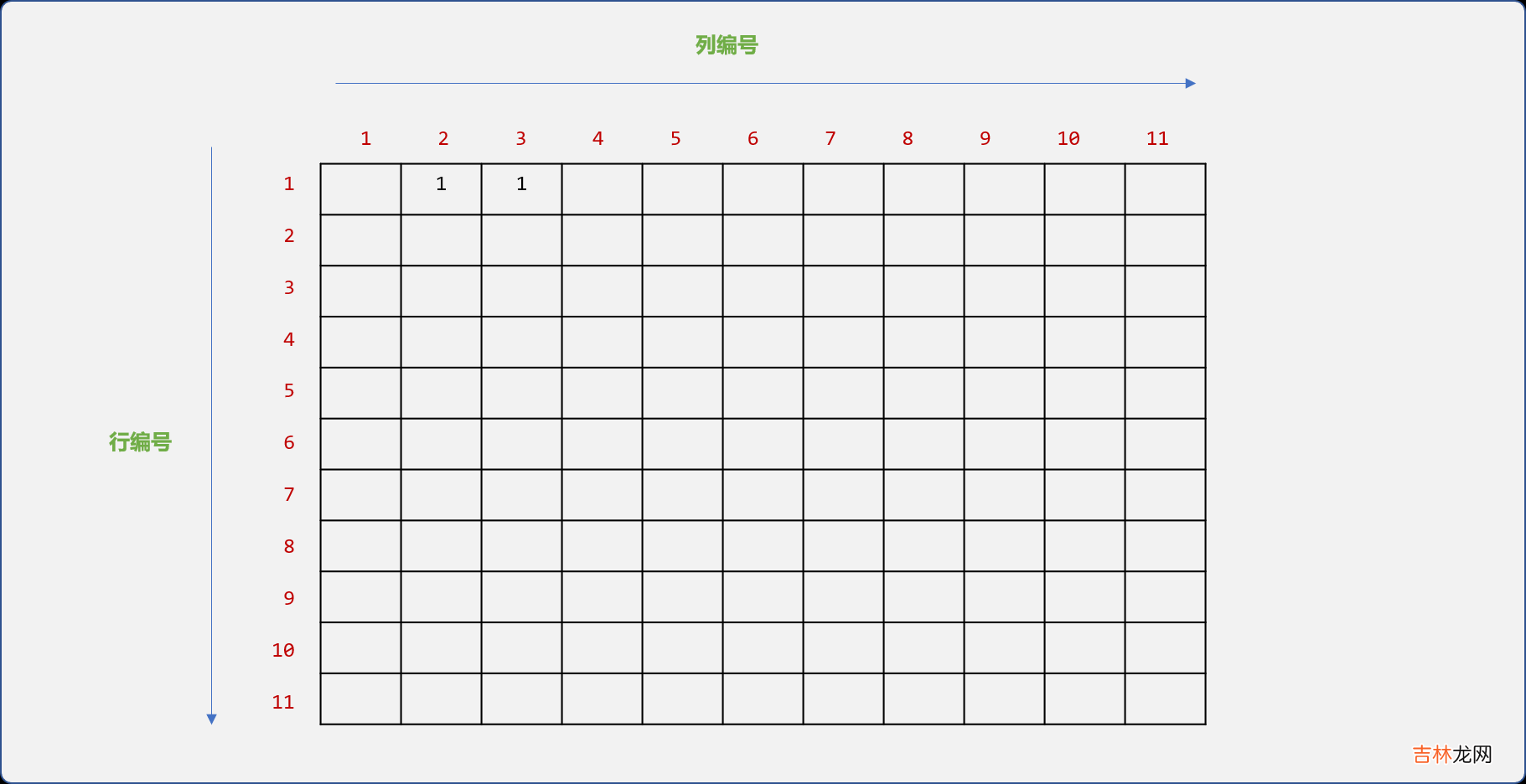
- 在树结构中,编号为
1的节点和编号为2、3的节点存在父子关系,则把矩阵的arrTree[1][2]和arrTree[1][3]的位置设置为1。也就是说,行号和列号交叉位置的值如果是1,则标志着编号和行号、列号相同的节点之间有关系 。
文章插图
- 找到树中所有结点之间的关系,最后矩阵中的信息如下图所示 。
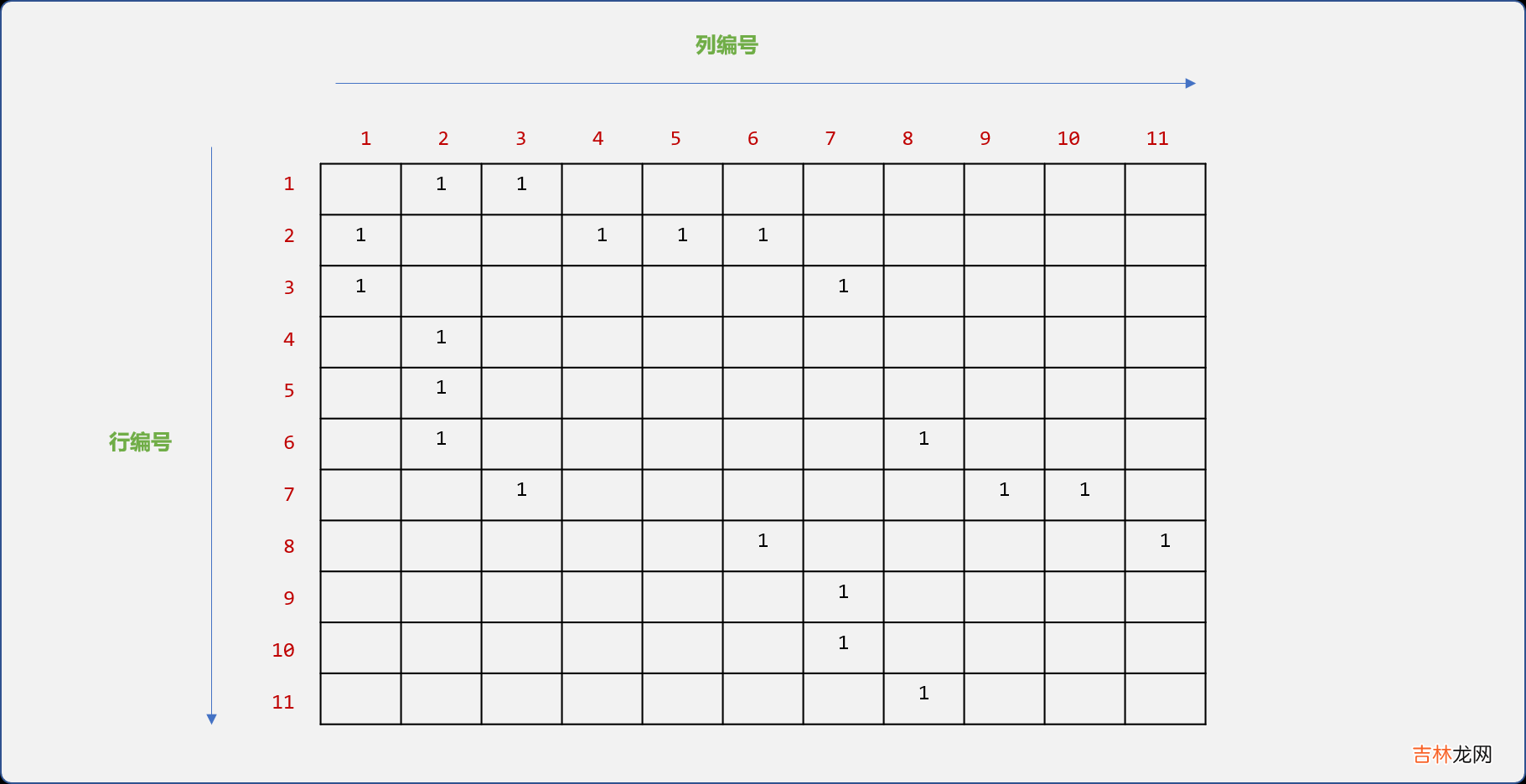
文章插图
矩阵记录了结点之间的双向(父到子,子到父)关系,最终看到是一个对称的稀疏矩阵 。可以只存储上三角或下三角区域的信息,并可以对矩阵进行压缩存储 。
邻接矩阵存储优点是实现简单、查询方便 。但是,如果不使用压缩算法,空间浪费较大 。
3.1.2 编码实现现采用邻接矩阵方案实现对如下树的具体存储:
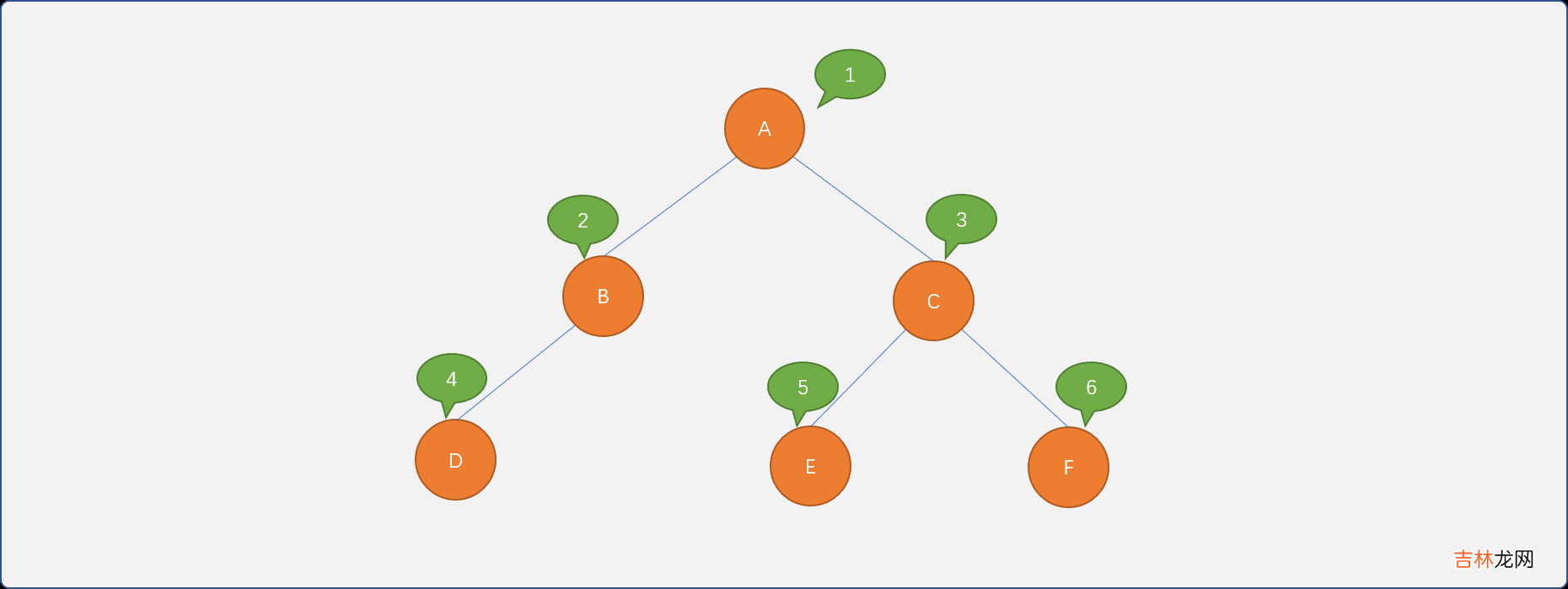
文章插图
- 节点类型: 用来描述数据的信息 。
struct TreeNode{ //节点的编号 int code; //节点上的值 int data;};- 树类型:树类型中除了存储节点(数据)信息以及节点之间的关系,还需要提供相应的数据维护算法 。本文仅考虑如何对树进行存储 。
class Tree { private:int size=7;vector<TreeNode> treeNodes;//使用矩阵存储节点之间的关系,矩阵第一行第一列不存储信息int matrix[7][7];//节点编号,为了方便,从 1 开始int idx=1; public:Tree() {}//初始根节点Tree(char root) {cout<<3<<endl;for(intr=1; r<this->size; r++) {for(int c=1; c<this->size; c++) {this->matrix[r][c]=0;}}TreeNode node= {this->idx,root};this->treeNodes.push_back(node);//节点的编号由内部指定this->idx++;}//获取到根节点TreeNode getRoot() {return this->treeNodes[0];}//添加新节点int addVertex(char val) {if (this->idx>=this->size)return 0;TreeNode node= {this->idx,val};this->treeNodes.push_back(node);//返回节点编号return this->idx++;;}/** 添加节点之间的关系*/bool addEdge(int from,int to) {char val;//查找编号对应节点是否存在if (isExist(from,val) && isExist(to,val)) {//建立关系this->matrix[from][to]=1;//如果需要,可以打开双向关系//this->matrix[to][from]=1;}}//根据节点编号查询节点bool isExist(int code,char & val) {for(int i=0; i<this->treeNodes.size(); i++) {if (this->treeNodes[i].code==code) {val=this->treeNodes[i].data;return true;}}return false;}//输出节点信息void showAll() {cout<<"矩阵信息"<<endl;for(intr=1; r<this->size; r++) {for(int c=1; c<this->size; c++) {cout<<this->matrix[r][c]<<" ";}cout<<endl;}cout<<"所有节点信息:"<<endl;for(int i=0; i<this->treeNodes.size(); i++) {TreeNode tmp=this->treeNodes[i];cout<<"节点:"<<tmp.code<<"-"<<tmp.data<<endl;//以节点的编号为行号,在列上扫描子节点char val;for(int j=1; j<this->size; j++ ) {if(this->matrix[tmp.code][j]!=0) {isExist(j,val);cout<<"\t子节点:"<<j<<"-"<<val<<endl;}}}}};
经验总结扩展阅读
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
- 2023年2月4日游玩好吗 2023年2月4日是游玩的黄道吉日吗
- C#实现生成Markdown文档目录树
- 2023年9月29日修理仓库黄道吉日 2023年9月29日是修理仓库的黄道吉日吗
- 2023年9月29日是打地基的黄道吉日吗 2023年9月29日打地基好吗
- 2023年9月29日是建造厕所的黄道吉日吗 2023年9月29日建造厕所好不好
- 2023年9月29日投资黄道吉日 2023年9月29日是投资的黄道吉日吗
- 2023年2月4日是做买卖的黄道吉日吗 2023年2月4日做买卖行吗
- 2023年9月29日是签订合同吉日吗 2023年9月29日是签订合同的黄道吉日吗
- 2023年2月4日安装柱子黄道吉日 2023年2月4日是安装柱子的黄道吉日吗
- 2023年9月29日就职好吗 2023年9月29日是就职的黄道吉日吗