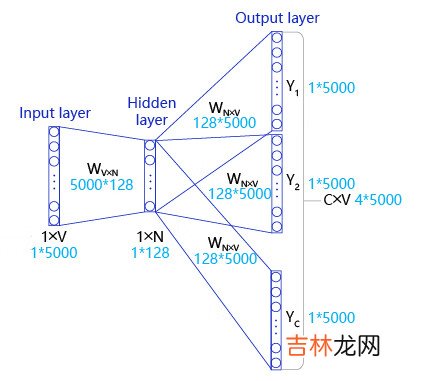
图学习参考资料词向量word2vec( 三 ) _生活百科

输出层：创建另一个形状为N×V的参数张量，将隐藏层得到的1×N的向量乘以该N×V的参数张量，得到了一个形状为1×V的向量。最终，1×V的向量代表了使用上下文去推理中心词，每个候选词的打分，再经过softmax函数的归一化，即得到了对中心词的推理概率：

$$({O_i})= \frac{exp({O_i})}{\sum_jexp({O_j})}$$
如图6 所示，Skip-gram是一个具有3层结构的神经网络，分别是：

文章插图

Input Layer（输入层）：接收一个one-hot张量 $V \in R^{1 \times \text{vocab_size}}$ 作为网络的输入，里面存储着当前句子中心词的one-hot表示。
Hidden Layer（隐藏层）：将张量$V$乘以一个word embedding张量$W_1 \in R^{\text{vocab_size} \times \text{embed_size}}$，并把结果作为隐藏层的输出，得到一个形状为$R^{1 \times \text{embed_size}}$的张量，里面存储着当前句子中心词的词向量。
Output Layer（输出层）：将隐藏层的结果乘以另一个word embedding张量$W_2 \in R^{\text{embed_size} \times \text{vocab_size}}$，得到一个形状为$R^{1 \times \text{vocab_size}}$的张量。这个张量经过softmax变换后，就得到了使用当前中心词对上下文的预测结果。根据这个softmax的结果，我们就可以去训练词向量模型。

在实际操作中，使用一个滑动窗口（一般情况下，长度是奇数），从左到右开始扫描当前句子。每个扫描出来的片段被当成一个小句子，每个小句子中间的词被认为是中心词，其余的词被认为是这个中心词的上下文。
2.1.1 Skip-gram的理想实现使用神经网络实现Skip-gram中，模型接收的输入应该有2个不同的tensor：

代表中心词的tensor：假设我们称之为center_words $V$，一般来说，这个tensor是一个形状为[batch_size, vocab_size]的one-hot tensor，表示在一个mini-batch中，每个中心词的ID，对应位置为1，其余为0 。
代表目标词的tensor：目标词是指需要推理出来的上下文词，假设我们称之为target_words $T$，一般来说，这个tensor是一个形状为[batch_size, 1]的整型tensor，这个tensor中的每个元素是一个[0, vocab_size-1]的值，代表目标词的ID 。

在理想情况下，我们可以使用一个简单的方式实现skip-gram 。即把需要推理的每个目标词都当成一个标签，把skip-gram当成一个大规模分类任务进行网络构建，过程如下：

声明一个形状为[vocab_size, embedding_size]的张量，作为需要学习的词向量，记为$W_0$ 。对于给定的输入$V$，使用向量乘法，将$V$乘以$W_0$，这样就得到了一个形状为[batch_size, embedding_size]的张量，记为$H=V×W_0$ 。这个张量$H$就可以看成是经过词向量查表后的结果。
声明另外一个需要学习的参数$W_1$，这个参数的形状为[embedding_size, vocab_size] 。将上一步得到的$H$去乘以$W_1$，得到一个新的tensor $O=H×W_1$，此时的$O$是一个形状为[batch_size, vocab_size]的tensor，表示当前这个mini-batch中的每个中心词预测出的目标词的概率。
使用softmax函数对mini-batch中每个中心词的预测结果做归一化，即可完成网络构建。

2.1.2 Skip-gram的实际实现然而在实际情况中，vocab_size通常很大（几十万甚至几百万），导致$W_0$和$W_1$也会非常大。对于$W_0$而言，所参与的矩阵运算并不是通过一个矩阵乘法实现，而是通过指定ID，对参数$W_0$进行访存的方式获取。然而对$W_1$而言，仍要处理一个非常大的矩阵运算（计算过程非常缓慢，需要消耗大量的内存/显存）。为了缓解这个问题，通常采取负采样（negative_sampling）的方式来近似模拟多分类任务。此时新定义的$W_0$和$W_1$均为形状为[vocab_size, embedding_size]的张量。