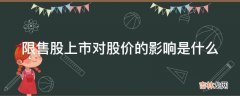
菱形的性质

1、对角线互相垂直且平分,并且每条对角线平分一组对角 。
2、菱形既是轴对称图形 , 对称轴是两条对角线所在直线 , 也是中心对称图形 。
3、菱形是特殊的平行四边形,它具备平行四边形的一切性质 。
【菱形的性质,菱形的四种性质和五种判定】
4、四条边都相等 。
5、对角相等,邻角互补 。
6、在60°的菱形中,短对角线等于边长,长对角线是短对角线的根号三倍 。
菱形的四种性质和五种判定
菱形的性质:1:对边相等且平行;
2:对角线互相垂直且平分;
3:对角相等;
4:对角线平分一组对角;
5:邻角互补;
6:邻边相等 。
菱形的判定:
1:邻边相等的平行四边形;
2:对角线互相垂直的平行四边形;
3:一条对角线平分一组对角的平行四边形 。
菱形的性质是什么
菱形的性质1、对角线互相垂直且平分,并且每条对角线平分一组对角;
2、四条边都相等;
3、对角相等,邻角互补;
4、菱形既是轴对称图形 , 对称轴是两条对角线所在直线,也是中心对称图形,
5、在60°的菱形中,短对角线等于边长 , 长对角线是短对角线的√3倍 。
6、菱形是特殊的平行四边形 , 它具备平行四边形的一切性质 。
菱形的基本判定
1、一组邻边相等的平行四边形是菱形
2、四边相等的四边形是菱形
3、对角线互相垂直且平分的四边形是菱形
不管原四边形的形状怎样改变,中点四边形的形状始终是平行四边形 。菱形的中点四边形是矩形(对角线互相垂直的四边形的中点四边形定为菱形,对角线相等的四边形的中点四边形定为矩形 。)
菱形是在平行四边形的前提下定义的,首先它是平行四边形,但它是特殊的平行四边形,特殊之处就是“有一组邻边相等” , 因而就增加了一些特殊的性质和不同于平行四边形的判定方法 。
菱形的定义、性质、判定是什么
菱形定义:有一组邻边相等的平行四边形叫做菱形 。菱形性质:
菱形除了具有平行四边形的一切性质外,还有一些特殊性质:
1.菱形的四条边都相等;
2.菱形的两条对角线互相垂直 , 并且每一条对角线平分一组对角.
3.菱形也是轴对称图形,有两条对称轴(对角线所在的直线),对称轴的交点就是对称中心.
菱形判定:
1.定义法:有一组邻边相等的平行四边形是菱形.
2.对角线互相垂直的平行四边形是菱形.
3.四条边相等的四边形是菱形.
菱形的性质是什么
菱形的性质:1、菱形具有平行四边形的一切性质;
2、菱形的四条边都相等;
3、菱形的对角线互相垂直平分且平分每组对角;
4、菱形是轴对称图形,对称轴有2条,即两条对角线所在直线;
5、菱形是中心对称图形 。
扩展资料:
判定:
一组邻边相等的平行四边形是菱形;
对角线互相垂直的平行四边形是菱形;
四条边均相等的四边形是菱形;
对角线互相垂直平分的四边形;
两条对角线分别平分每组对角的四边形;
有一对角线平分一个内角的平行四边形;
菱形是在平行四边形的前提下定义的 , 首先它是平行四边形,而且是特殊的平行四边形 , 特殊之处就是“有一组邻边相等”,因而增加了一些特殊的性质和判定方法 。
菱形的一条对角线必须与x轴平行,另一条对角线与y轴平行 。不满足此条件的几何学菱形在计算机图形学上被视作一般四边形 。
资料来源:头条百科https://www.baike.com/wiki/%E8%8F%B1%E5%BD%A2?search_id=3z2q5a8ls4e000&prd=search_sug&view_id=28nv6xp53rgg00
以上就是关于菱形的性质,菱形的四种性质和五种判定的全部内容,以及菱形的性质的相关内容,希望能够帮到您 。