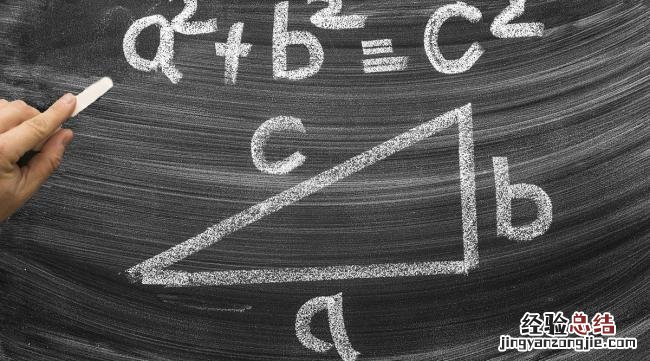
勾股定理:在任何一个平面直角三角形中的两直角边的平方之和一定等于斜边的平方 。在△ABC中,∠C=90°,则a2+b2=c2 。勾股定理,是几何学中一颗光彩夺目的明珠 , 被称为“几何学的基石”,而且在高等数学和其他学科中也有着极为广泛的应用 。
【勾股定理的公式变形 - 经验总结 www.jingyanzongjie.com】
?
1发展历程
中国是发现和研究勾股定理最古老的国家之一 。中国古代数学家称直角三角形为勾股形 , 较短的直角边称为勾,另一直角边称为股,斜边称为弦,所以勾股定理也称为勾股弦定理 。在公元前1000多年 , 据记载,商高(约公元前1120年)答周公曰“故折矩 , 以为勾广三,股修四,径隅五 。既方之,外半其一矩 , 环而共盘,得成三四五 。两矩共长二十有五,是谓积矩 。”因此,勾股定理在中国又称“商高定理” 。在公元前7至6世纪一中国学者陈子,曾经给出过任意直角三角形的三边关系:以日下为勾,日高为股 , 勾、股各乘并开方除之得斜至日 。
2主要意义
1、勾股定理是联系数学中最基本也是最原始的两个对象——数与形的第一定理 。
2、勾股定理导致不可通约量的发现,从而深刻揭示了数与量的区别,即所谓“无理数"与有理数的差别,这就是所谓第一次数学危机 。
3、勾股定理开始把数学由计算与测量的技术转变为证明与推理的科学 。
4、勾股定理中的公式是第一个不定方程,也是最早得出完整解答的不定方程,它一方面引导到各式各样的不定方程 , 另一方面也为不定方程的解题程序树立了一个范式 。











