输出结果:
1866163.后缀表达式后缀表达式也称为逆波兰式,其求解过程比中缀表达式要简单,整个过程只需要一个操作数栈 。所以往往会把中缀表达式转换成后缀表达式后再求解 。
后缀表达式的求解流程:
- 创建一个栈 。
- 把后缀表达式当成一个字符串,对字符串进行逐字符扫描 。
- 遇到操作数入栈,遇到运算符则从栈中取出
2个操作数,运算后把结果压入栈 。 - 重复上述过程,直到扫描结束 。则栈中的值为最终结果 。
8571-*+82/-的代码 。Tips:此后缀表达式对应的中缀表达式是:8+5*(7-1)-8/2
#include <iostream>#include <stack>using namespace std;int main() { char exp[20]="8571-*+82/-"; stack<int> expStack; int num1; int num2; char opt; int res; for(int i=0; exp[i]!='\0'; i++) {if (exp[i]>='0' && exp[i]<='9') {//入栈expStack.push(exp[i]-'0');} else {//出栈num1=expStack.top();expStack.pop();//出栈num2=expStack.top();expStack.pop();//运算符opt=exp[i];switch(opt) {case '+':res=num2+num1;break;case '-':res=num2-num1;break;case '*':res=num2*num1;break;case '/':res=num2/num1;break;}expStack.push(res);} } cout<<expStack.top()<<endl; return 0;}执行后的输出结果:344. 中缀转后缀表达式虽然后缀表达式的计算过程要比中缀表达式简单很多,前提条件是要先把中缀表达式转换成后缀表达式 。转换流程:
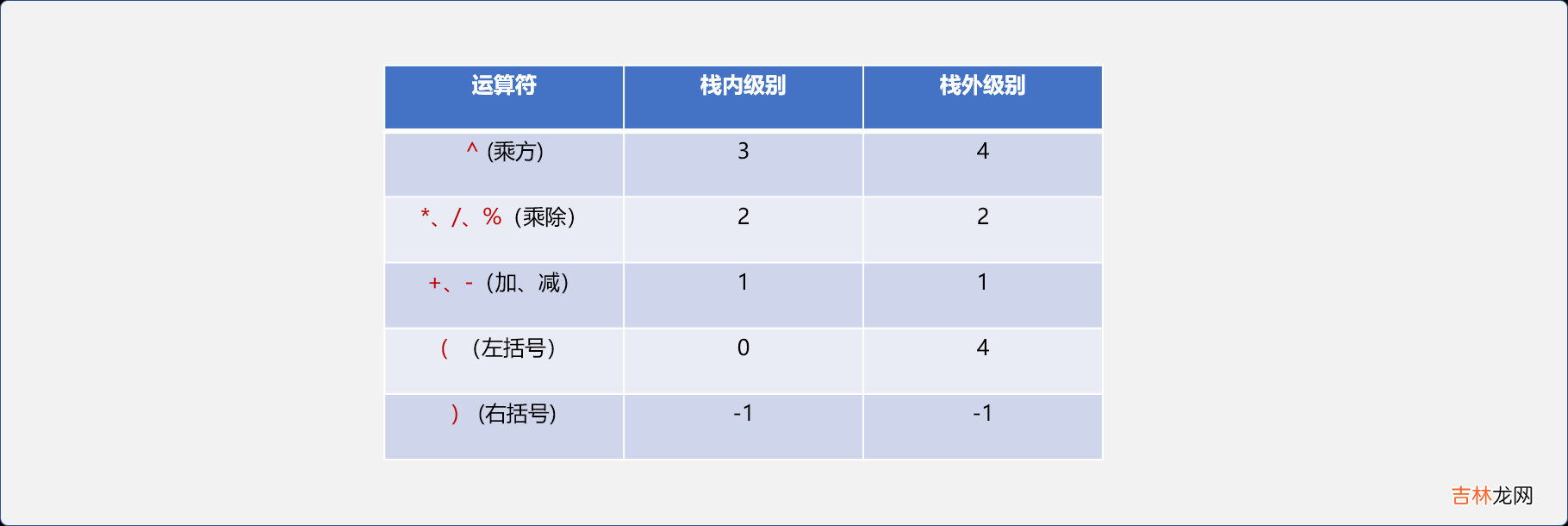
- 初始化一个运算符栈 。
- 自左向右扫描中缀表达式,当扫描到操作数时直接连接到后缀表达式上 。
- 当扫描到操作符时,和运算符栈栈顶的操作符进行比较 。如果比栈顶运算符高,则入栈 。如果比栈顶运算符低,则把栈顶的运算符出栈后连接到中缀表达式上 。
- 若运算符是右括号,栈顶是左括号时,删除栈顶运算符(清除括号 。后缀表达式中是没有括号的,操作数后面的运算符的优先级由左向右降低) 。
- 重复以上过程直到遇到结束符 。
文章插图
4.1 流程演示如下把
8+5*(7-1)-8/2 中缀表达式转换成后缀表达式 。- 初始化运算符栈 。
文章插图
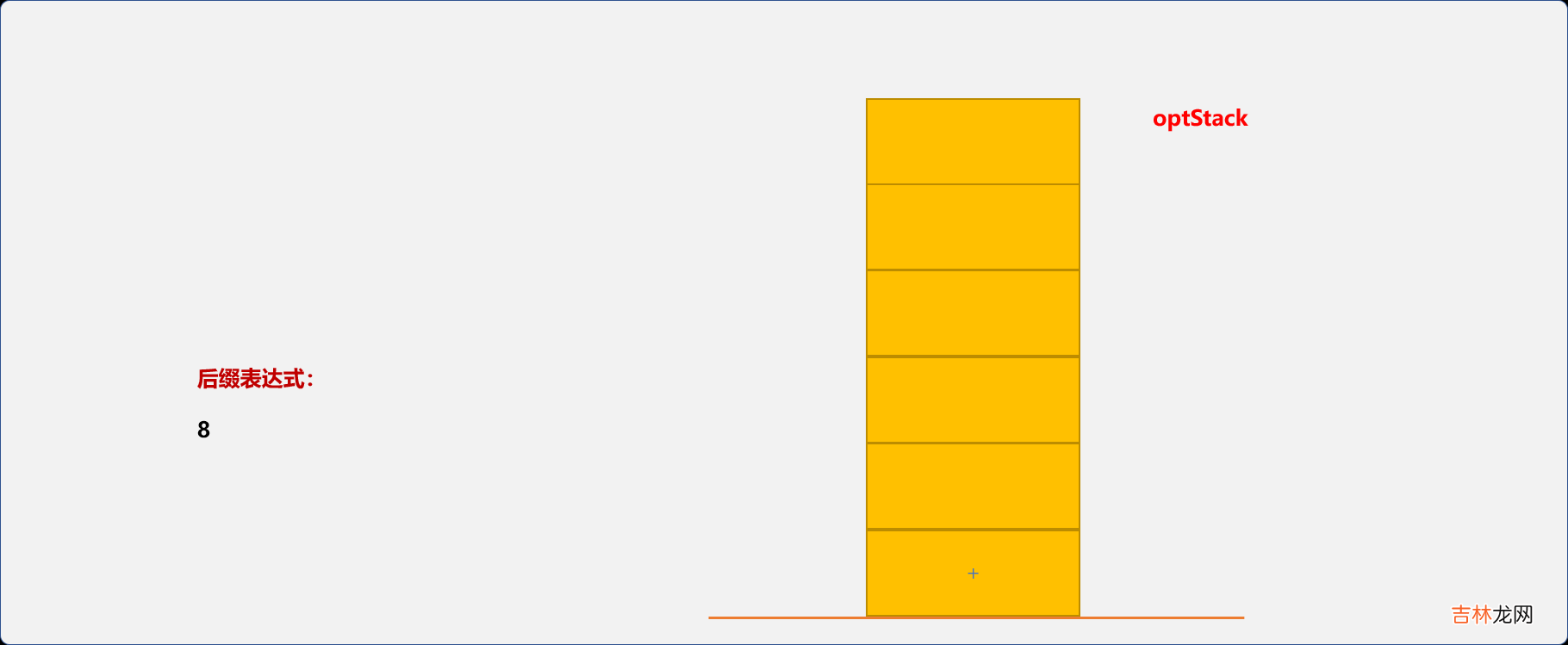
- 扫描中缀表达式,字符
8直接输出,+是第一个操作数,因可能后续有更高的运算符,入栈 。
文章插图
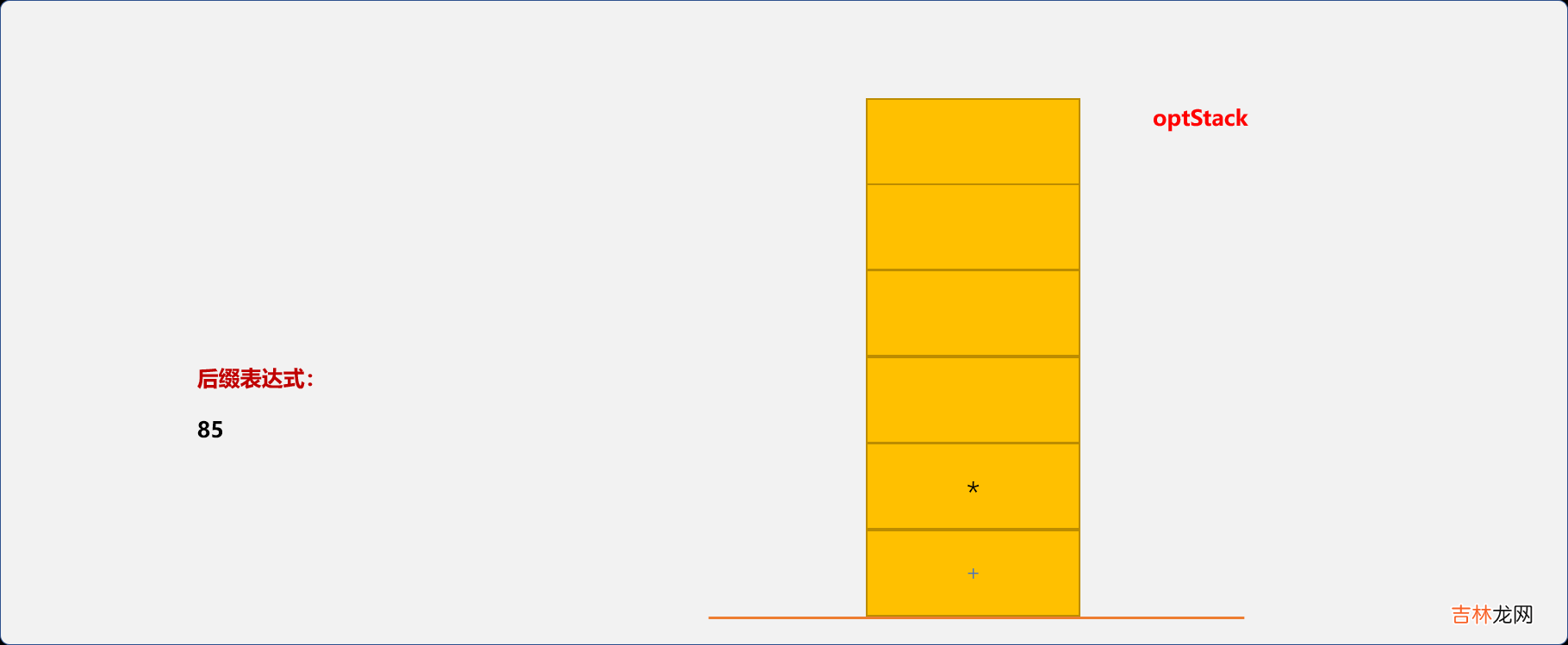
- 字符
5直接输出,*优先级大于栈顶+优先级,入栈 。
文章插图
(运算符在栈外优先级最高,入栈 。

文章插图
- 字符
7直接输出,因(运算符在栈内优先级最低,-运算符入栈 。

文章插图
- 字符
1直接输出,)栈外优先级最低 。运算符出栈,一直碰到(。
文章插图












