C.差分维护，D.容斥原理 CodeTON Round 3( 二 ) _生活百科

所以，问题可以转化为：从[1，m/a[i]]中选与（a[i-1]/a[i])互质的数有多少个
于是引入容斥原理：

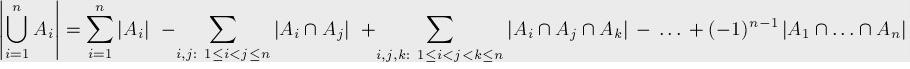
文章插图
Tot = C$_n$$^1$ - C$_n$$^2$ + C$_n$$^3$.....
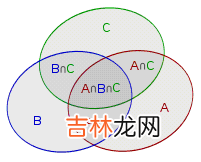
用韦恩图表示如下：

文章插图

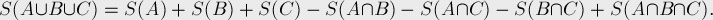
文章插图
所以我们就考虑用总的（m/a[i])-res（所有与a[i-1]/a[i]不互质的数的并集）
之所以取与a[i-1]/a[i]不互质的数的并集是因为它比较好表示，用（m/a[i])/（选中的因子的积)就是不互质数的数量比如从1,2,3,4,5,6中求与2,3不互质的数实际上就是6-（2的倍数（{2,4,6} $\rightarrow$6/2 = 3）+3的倍数（{3,6} $\rightarrow$6/3 = 2）-（2*3）的倍数（{6} $\rightarrow$6/6 = 1）） = 6-3-2+1 = 2{1,5}
代码实现：

【C.差分维护，D.容斥原理 CodeTON Round 3】

# include<iostream># include<bits/stdc++.h>using namespace std;# define int long long# define endl "\n"const int N = 2e5 + 10, mod = 998244353;int a[N];//在[1,top]范围内，找和n互质的数的个数int cal(int n,int top){	vector<pair<int,int>> divisors;//质因子	for(int i = 2;i*i<=n;++i){if(n%i == 0){int s= 0;while(n%i == 0) n/=i,s++;divisors.push_back({i,s});//i的s次}	}	if(n>1) divisors.push_back({n,1});	int res = 0,m = divisors.size();	for(int i = 1;i< (1<<m);++i)//二进制模拟第j个元素选还是不选{int t = 1,s = 0;for(int j = 0;j < m;++j){if(i>>j&1){if(t*divisors[j].first>top){t = -1;break;}t *= divisors[j].first;s++;}}if(t != -1){if(s%2) res += top/t;//如果选了奇数个元素就是加else res -= top/t;//偶数个元素是减//从容斥原理可以得到}	}	return top-res;}void solve() {	int n,m;	cin>>n>>m;	for(int i = 1;i <= n;++i) cin>>a[i];	for(int i = 2;i <= n;++i){if(a[i-1]%a[i]){cout<<0<<endl;return;}	}	int ans = 1;	for(int i = 2;i <= n;++i){if(a[i] == a[i-1]){ans = ans*(m/a[i])%mod;}else{int t = cal(a[i-1]/a[i],m/a[i]);ans = ans*t%mod;}	}	cout<<ans<<endl;}int tt;signed main() {	ios::sync_with_stdio(false);	cin.tie(0);	cout.tie(0);	tt = 1;	cin >> tt;	while (tt--)solve();	return 0;}