完全非弹性碰撞:在碰撞过程中动能损失最大,即动能不守恒,但动量仍然守恒,可以从数学证明,碰后两物体共速 , 完全非弹性碰撞的实例:碰撞后二者合为一体(比如粘贴在一起,子弹钻入木块内等) 。
如果只存在系统内相互作用(满足动量守恒或者单方向动量守恒),在动能损失最大的情况下,与完全非弹性碰撞类似,把这类情况称之为类完全非弹性碰撞 。
类完全非弹性碰撞特点:
①动能损失最大②共速
损失的动能为m?m?(v??-v??)2/2(m?+m?),损失的动能取决于初始的相对速度 。
例题:如图所示,

文章插图
【完全弹性碰撞一轮复习 完全弹性碰撞速度公式】 将两根完全相同的磁铁(磁性极强)分别固定在质量相等的小车上,水平面光滑.开始时甲车速度大小为3m/s , 乙车速度大小为2m/s , 两车速度方向相反并在同一条直线上.
(1)当乙车的速度为零时,甲车的速度是多少?方向如何?
(2)由于磁铁磁性极强,故两车不会相碰,则两车距离最短时乙车速度为多少?方向如何?
例题:如图所示,
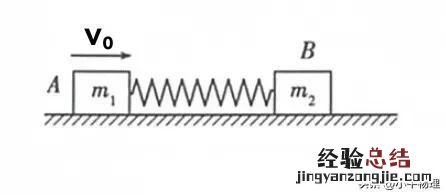
文章插图
一轻弹簧的两端与质量分别为m?和m?的两滑块A、B相连接,并静止在光滑的水平面上.现使滑块A瞬时获得水平向右的速度v?,在运动过程中,求:弹簧的弹性势能最大的时刻及最大值,以及滑块A的最小速度和滑块B的最大速度.
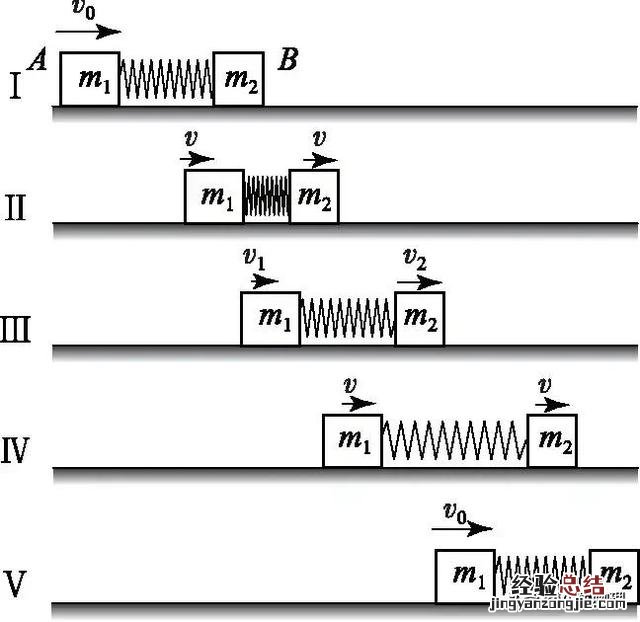
文章插图

文章插图
?对滑块A、B,在相互作用的过程中,相互作用的弹力(内力)使滑块A做减速运动,使滑块B做加速运动,当两者速度相同(滑块A相对滑块B的速度为零)时,弹簧压缩量最大(弹力最大),即滑块A从位置Ⅰ到位置Ⅱ,滑块A的动能转化为滑块B的动能和弹簧的弹性势能.此后弹力使滑块A继续减速,使滑块B继续加速,从图3位置Ⅱ到位置Ⅲ,滑块A的动能和弹簧的弹性势能又转化为滑块B的动能.但从图3位置Ⅰ到位置Ⅲ,总机械能不变,弹簧长度也不变,所以总动能也不变.同时系统无外力作用,故动量守恒.
例题:在同一平直铁轨上 , 有两节车厢,质量分别为m?=1×10?kg,m?=2×10?kg,求下列四种不同方式的挂接所损失的最大动能()
A.m?静止 , m?以2m/s的速度向右撞击 m?.
B.m?静止 , m?以2m/s的速度向左撞击 m?.
C.m?以1m/s的速度向右运动,m?以3m/s的速度向右追击m?
D.m?以1m/s的速度向右运动,m?以1m/s的速度向左运动与m?撞击
?四种撞击方式都认为是完全非弹性碰撞,动能损失最大取决于碰撞前的相对速度,碰撞前相对速度一样,所以损失动能相同 。
例题:如图所示,

文章插图
带电小球B静止在无限大的光滑绝缘水平面上,带同种电荷的小球A从很远处以初速度V?向B球运动,A的速度始终沿着两球的连线方向 。两球始终未能接触 。A、B间的相互作用视为静电作用 。已知A、B两球的质量分别为m?和m? 。求:
(1)A、B两球相互作用的过程中,它们之间电势能的最大值 。
(2)A、B两球最终的速度大小 。
例题:如图所示 ,

文章插图
在光滑水平面上放置一质量为M的足够长的光滑曲面,现有一质量为m的小球以初速度v?冲上曲面 , 则小球能够达到的最大高度h为多少?并讨论小球返回曲面左端时的速度?
【解析】
整个过程满足水平方向动量守恒,机械能守恒 。
小球上到最高点,重力势能最大,动能最小,动能损失最大,达到共速,类完全非弹性碰撞;小球返回最低点时,重力势能复原,动能没有损失,类完全弹性碰撞 。














