这是在今日头条上看到的几何题 。这种题目经常可以碰到,属于常考题目 。我们分析一下怎样去做 。
文章插图
常见几何题
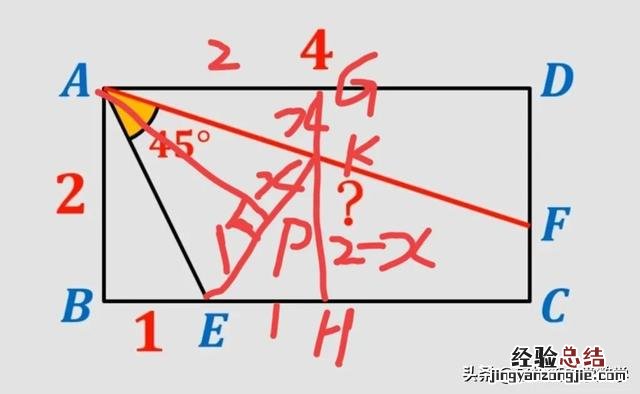
一个长方形 , AB=2,AD=4,BE=1,∠EAF=45°,求AE的长度 。
首先想到就是把长方形砍去一半,留下一个正方形,题目意思是一样的 。即ABHG是正方形,则AK=KF 。连接EK,作AP⊥EK,用旋转法易证PE=BE,GK=PK 。这是经常会碰到的题型,属于送分题 。
设GK=x,则KH=2-x,由勾股定理得:
KE2=KH2+EH2,
(x+1)2=(2-x)2+12 , 解方程得x=2/3 。
AK=2√10/3,AF=4√10/3 。证毕 。
高中学生用余弦定理也可以很快做出 。
对△AEK用余弦定理:
(x+1)2=x2+4+5-2√5√(x2+4)cos45°,
化简得:
3x2+16x-24=0,x=2/3 。后面同上 。
【三种方法解决一道几何经典题 如何有效的分析几何题】 再来看老师的解答 。老师的解答是把长方形放大一倍成为一个正方形,解题思路是一样的,都是把长方形构造成正方形来解 。

文章插图
老师的解答
这种题型是常考题 , 比较简单,希望大家都会做 。












