其中,$\gamma$ 和 $\beta$ 是可学习参数 。
最后再执行 concat。
2.1.5 Graph Convolution Module
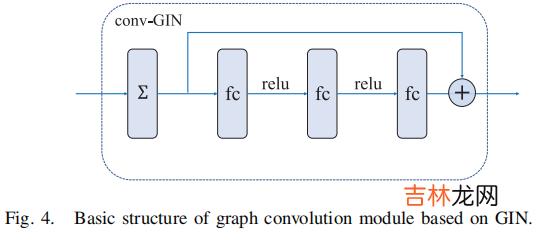
文章插图
GCN 可以编码局部图的结构和节点特征 。其正向传播公式如下:
$H^{(l+1)}=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} H^{(l)} W^{(l)}\right) \quad\quad\quad(8)$
由于 GCN 存在无法识别 multiset 的情况, 所以本文使用 GIN backbone :$w_{v}^{k}=N N^{k}\left(\left(1+\varepsilon^{k}\right) \cdot w_{v}^{k-1}+\sum\limits _{u \in N(v)} w_{u}^{k-1}\right)$
最后,将通过 GIN 生成的节点向量放入一个 $3$ 层的全连接网络,并加入残差结构:$\widetilde{w}=w+F(w)$2.1.6 Pooling Module常见的池化操作包括 average pooling 和 maximum pooling,分别如 $\text{Eq.11}$ $\text{Eq.12}$ 所示:
$\begin{array}{l}h_{G}=\frac{1}{m} \sum\limits _{i=0}^{m} \widetilde{w_{i}} \\h_{G}=\max \left(\widetilde{w_{0}}, \widetilde{w_{1}}, \ldots, \widetilde{w_{m}}\right)\end{array}$
平均池化是为了获得图中所有节点的平均向量作为图向量,最大池化是选择此维度中所有节点的最大值作为每个维度的输出 。
Note:一种新的池化方案,先将节点的表示向量按值降序排列后,选择顶部的 $k$ 个节点,拼接 $k$ 节点向量后,采用一维卷积法进行特征压缩,压缩后的向量为最终的图表示 。
本文采取的池化过程:将GIN 每层的输入进行concat ,然后使用 Note 中的池化策略 。
$h_{G}=\operatorname{Pooling}\left(\text { Concat }\left(\left\{\widetilde{w_{v}^{k}} \mid k=0,1, \ldots, K\right\}\right) \mid v \in V\right)$
最后使用 $h_{G}$ 进行分类:$\hat{y}=\operatorname{softmax}\left(F C\left(h_{G}\right)\right)$3 ExperimentDataset
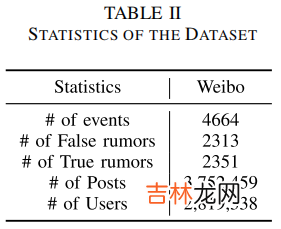
文章插图
Results
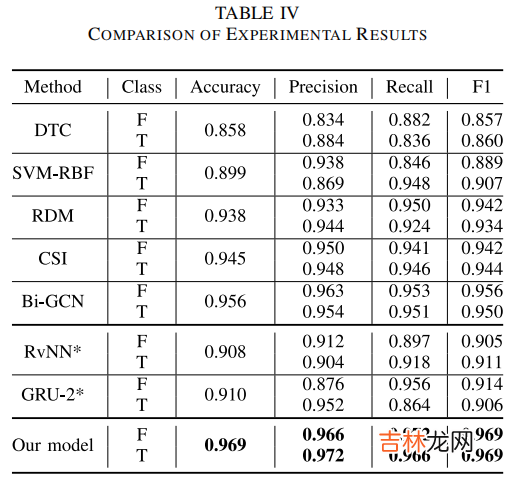
文章插图
【谣言检测《Data Fusion Oriented Graph Convolution Network Model for Rumor Detection》】
经验总结扩展阅读
- 赠花卿的诗意
- 有没有女主很漂亮柔弱的小说
- 什么歌好听又好唱
- 求女主特别nb的星际科幻文
- 重生耽美发家致富文8090年代
- 有什么好看的书类似于无声告白
- 考试什么的都去死吧本兮是翻唱吗
- 王牌对王牌阿Sa是哪一期?
- 电视剧独步天下角色介绍?
- 电视剧猎场演员表介绍?
















