京东云开发者｜经典同态加密算法Paillier解读 - 原理、实现和应用 _生活百科

文章插图
摘要随着云计算和人工智能的兴起，如何安全有效地利用数据，对持有大量数字资产的企业来说至关重要。同态加密，是解决云计算和分布式机器学习中数据安全问题的关键技术，也是隐私计算中，横跨多方安全计算，联邦学习和可信执行环境多个技术分支的热门研究方向。
本文对经典同态加密算法Pailier算法及其相关技术进行介绍，重点分析了Paillier的实现原理和性能优化方案，同时对基于公钥的加密算法中的热门算法进行了横向对比。最后介绍了Paillier算法的一些实际应用。
【关键词】：同态加密，多方安全计算，联邦学习，隐私计算
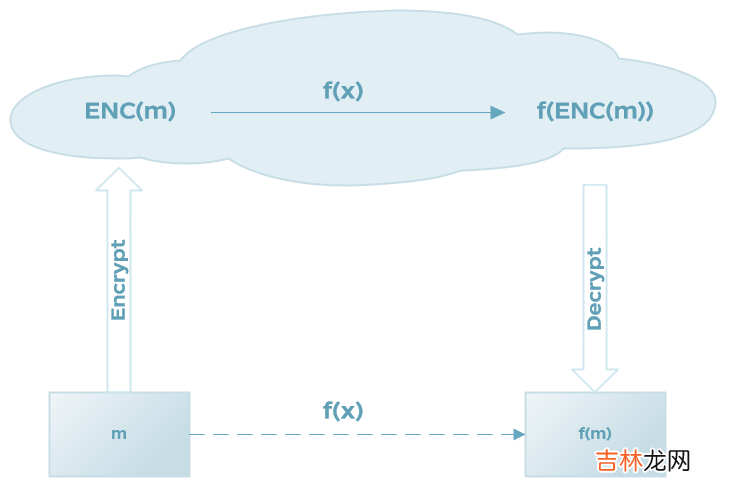
1 背景知识1.1 同态加密同态加密（Homomorphic Encryption，HE）[1]是将数据加密后，对加密数据进行运算处理，之后对数据进行解密，解密结果等同于数据未进行加密，并进行同样的运算处理。同态加密的概念最初在1978年，由Ron Rivest，Leonard Adleman和Michael L. Dertouzos共同提出，旨在解决在不接触数据的前提下，对数据进行加工处理的问题。
目前，同态加密支持的运算主要为加法运算和乘法运算。按照其支持的运算程度，同态机密分为半同态加密（Partially Homomorphic Encryption, PHE）和全同态加密（Fully Homomorphic Encryption, FHE）。半同态加密在数据加密后只持加法运算或乘法运算中的一种，根据其支持的运算的不同，又称为加法同态加密或乘法同态加密。半同态加密由于机制相对简单，相对于全同态加密技术，拥有着更好的性能。全同态加密对加密后的数据支持任意次数的加法和乘法运算。
1.2 复合剩余类问题【京东云开发者｜经典同态加密算法Paillier解读 - 原理、实现和应用】如果存在一个数

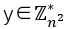
文章插图
那么符合公式z ≡ yn (mod n2)的数z，称为y的模n2的n阶剩余。复合剩余类问题（decisional composite residuosity assumption , DCRA)，指的是给定一个合数n和整数z，很难确定模n2的n阶剩余数z是否存在。
1.3 中国剩余定理中国剩余定理（Chinese Remainder Theorem, CRT），又称为孙子定理，源于《孙子算经》，是数论中的一个关于一元线性同余方程组的定理，说明了一元线性同余方程组有解的准则以及求解方法。
有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二。问物几何？翻译为数学语言为：

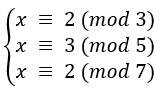
文章插图
其通用方程为：

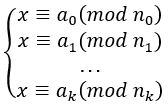
文章插图
中国剩余定理的解法流程为：

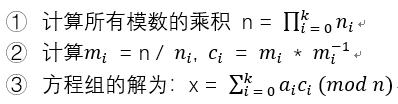
文章插图
2 Paillier算法原理2.1 Paillier简介在Paillier算法出现之前，基于公钥加密的算法主要有两个分支：

以RSA为代表的，基于大数因数分解难题的公钥加密算法
以ElGama为代表的，基于大数离散对数难题的公钥加密算法

Paillier加密算法，由Pascal Paillier于1999年发表，给出了公钥加密算法的一个新的分支领域。Paillier基于复合剩余类难题，满足加法同态和数乘同态，具有非常高效的运行时性能。
2.2 一个典型的应用场景

文章插图
图1 传统联邦学习同态加密算法使得密文数据，在没有额外数据泄露的情况下，可以在第三方平台进行进一步加工处理。随着大规模云计算的兴起，尤其是涉及到敏感数据的云计算，同态加密算法将是其中至关重要的技术基础。我们以一个典型的联邦学习的例子为切入点，看看Paillier算法的原理和在实践中应用的问题。