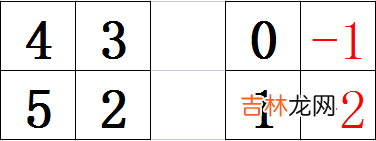
susliks 打地鼠方法记录( 二 ) _生活百科

但是，如果出现下面这种，左上角的数清零导致区域内其它数变成负数的情况，就可以直接判断出这种型号的锤子无法满足要求，然后直接枚举下一种锤子的型号。

文章插图
若有一种型号的锤子能锤遍全图，我们再判断一下全图中是否还有元素未被清零。若有，则说明这个型号的锤子无法满足要求，否则，计入最小答案。
显然，由于思路2需要枚举的砸击次数少，且能及时排除不合要求的锤子，所以思路2更优
然后再考虑其它优化手段。
假设一把 \(r\times c\) 的锤子是合格的，它需要砸 \(x\) 次，那么它总共砸毙的地鼠数 \(sum=r\times c\times x\)，这个\(sum\) 我们可以事先统计出来，即全部地洞里的地鼠数量之和。
换个角度来想，我们已经统计出 \(sum\)，现在正在枚举 \(i\times j\) 型号的锤子。若这种锤子满足要求，就应该满足：\(sum\) 是\(i\times j\) 的整数倍。在此基础上再判断该型号的锤子能否锤尽全图地鼠，若能，则答案 \(ans=sum/i/j\) .可以节省不少时间。这里枚举 \(i\) 和 \(j\) ,就可以从\(1\)~\(n\) 进行，这样 \(i\) 和 \(j\) 越枚举越大，\(ans\) 也就越来越小，省去了比较大小的过程。
除此之外我们还可以进行剪枝。
若当前的 \(sum/i/j\) 小于已经算出来的 \(ans\)，则当前情况必不可能为最优情况。
AC代码：

#include<iostream>#include<cstdio>#include<cstring>#include<algorithm>using namespace std;const int N=105;int a[N][N],b[N][N],n,m,ans,sum;bool check(int x,int y){	memcpy(b,a,sizeof(a));	for(int i=1;i<=n-x+1;i++)	{for(int j=1;j<=m-y+1;j++){if(b[i][j]){int z=b[i][j];for(int k=0;k<x;k++){for(int l=0;l<y;l++){b[i+k][j+l]-=z;if(b[i+k][j+l]<0) return 0;}}}}	}	for(int i=1;i<=n;i++)	{for(int j=1;j<=m;j++){if(b[i][j]) return 0;}	}	return 1;}int main(){	scanf("%d%d",&n,&m);	for(int i=1;i<=n;i++)	{for(int j=1;j<=m;j++){scanf("%d",&a[i][j]);sum+=a[i][j];}	}	ans=sum;	for(int i=1;i<=n;i++)	{for(int j=1;j<=m;j++){if(sum%(i*j)==0&&sum/i/j<ans){if(check(i,j)) ans=sum/i/j;}}	}	printf("%d\n",ans);	return 0;}

【susliks 打地鼠方法记录】