质能方程，爱因斯坦质能方程的详细推导_知道经验

本文较为硬核，请酌情跳过部分内容。
你之前看到的推导过程基本上从一开始就错了。

网上流传的推导方法很多，不过几乎都不是爱因斯坦在1905年的论文中的推导过程。
既然问题中提到了“爱因斯坦的质能方程”，那我就介绍一下爱因斯坦本人的推导方法。这种推导方法非常简单，而且能很好地反应出物理学各个分支的统一性。
然后再谈一下典型的反面教材，也就是从质速关系开始推导的方法，这种推导方法流传甚广，但却是在循环论证。

爱因斯坦的最初推导
物体的惯性同它所包含的能量有关吗？
这是爱因斯坦在1905年写的一篇论文的标题，其中有一个简单的推导过程，不过为了让大家看得更明白，本文把推导过程进一步简化并加入一些额外的说明。

这与原文有出入，但是思路是一样的。

想象一个物体，在某个参考系（参考系1）中静止，此时它的能量是E0，然后它向两个相反的方向各发射了一个光子，这两个光子的能量相同，两个光子的总能量是L 。
两个光子的能量相同，就说明动量也相同，所以物体依然静止，发射光子之后的物体的能量是E1 。

现在换一个参考系（参考系2），重新看待上面的过程。在这个参考系中物体原本做匀速直线运动，能量是H0，然后它向运动方向的前后各发射了一个光子。
发射光子之后的物体依然做匀速直线运动，此时物体的能量是H1 。

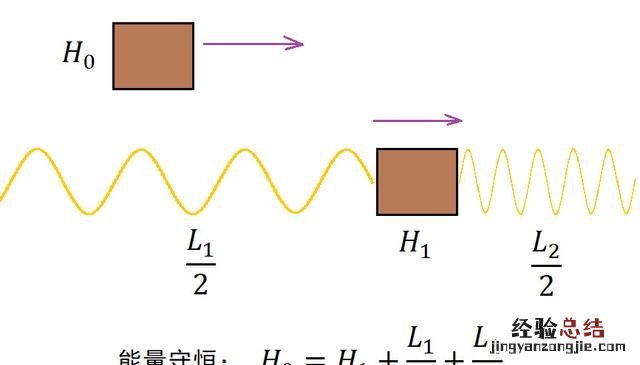
接下来就要把两个参考系中的能量守恒方程联系起来，联系的途径就是光。
光子的能量和频率成正比，这就是普朗克公式，具有普遍意义，在这里可以使用（别以为这个公式只能在量子力学里出现）。

在参考系1中，两个光子的能量相同，所以频率也相同。而在参考系2中，光会产生多普勒效应，这会使参考系2中的光子频率和参考系1中的光子频率不同。
不同参考系中的光的频率的计算公式可以用简单的分析和“钟慢效应”的公式得到，在这里就直接使用了，感兴趣的读者可以看我之前写的文章，评论区里会附上链接。

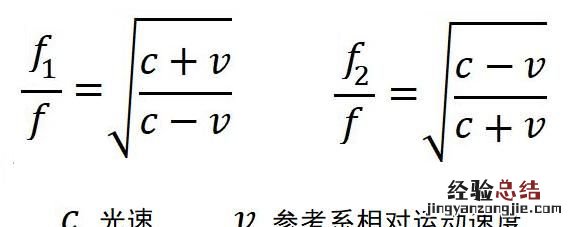
根据普朗克公式可以知道，光子的能量之比就等于频率之比，这就可以让参考系1和参考系2中的光子能量建立联系。

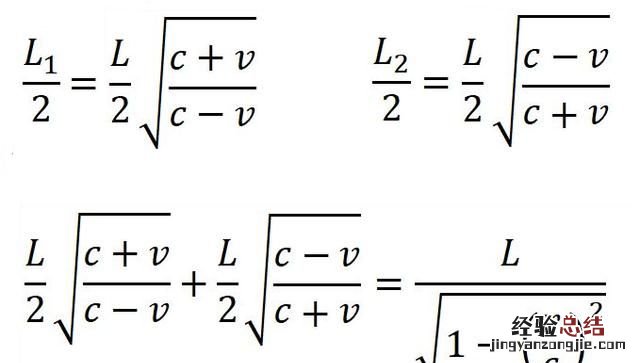
我们可以重新写出两个参考系中的能量守恒方程：

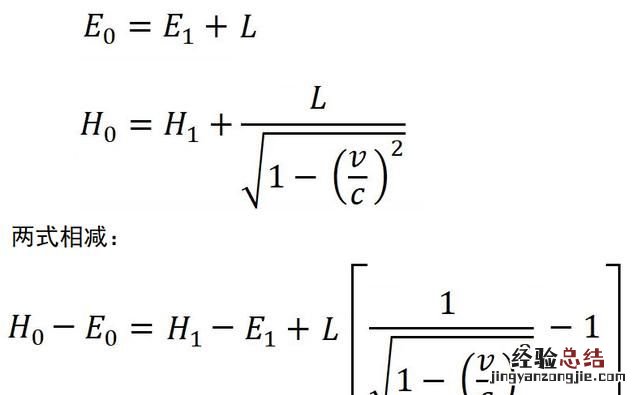
然后就需要做一些近似，把参考系2中的光子能量公式做一个被称为“麦克劳林展开”的操作，大家不必对这个操作感到恐慌，其实我们常用的十进制数字就使用了类似的思想。

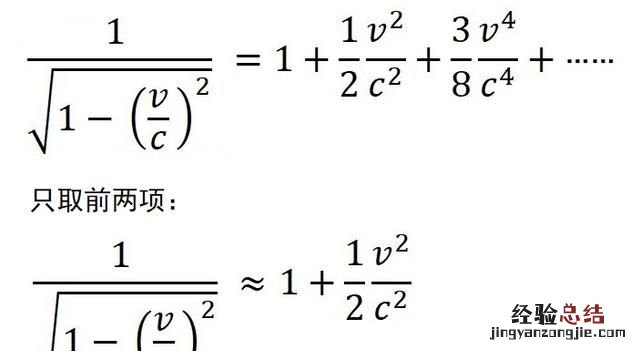
做了近似之后，经典力学中的动能公式也可以借用一下，物体在参考系2中的能量应该比参考系1中的能量多了动能。

然后我们就可以发现其中的一个式子似乎可以理解成质量。

物体发射光子，不仅发出了能量，还发出了质量，并且发出的能量和质量之比是光速的平方！
没有简单的严格推导
上面的推导过程可能让很多读者都无法满意，这很正常，因为它本身就不是一个严谨的推导过程，仅仅只是相对论力学的萌芽时期的探索。
爱因斯坦在1907年的论文（关于相对性原理和由此得出的结论）里面写了严格的推导过程，不过很复杂。
所有严格的推导过程都要用到麦克斯韦方程组和洛伦兹力公式，“动体的电动力学”可不是白叫的，没有受过专门的训练是理解不了的，在这里就不提了。
典型的反面教材（质速关系）
大部分人都在使用下面这张图片的推导过程，把质速关系式当成了前提条件。

那么质速关系式是怎么推导出来的？
有些人会说：

为了在相对论的速度叠加公式下保证不同参考系中的动量守恒定律都成立，要让质量随速度变化，得出质速关系式。

不过大部分这么说的人只是说说而已，根本不展示具体的推导过程。我也从没见过有人真的按照这个思路推导出质速关系式。
当然，有人真的按照这个思路做过推导，不过是在瞎推导，推导过程中，质量一会儿与速度有关，一会儿又与速度无关，纯粹是胡乱凑出了质速关系式。

注意，用上面的思路是推导不出质速关系的，要是能推导出来就违背相对论了（具体内容在下一小节介绍）。
而且质速关系式是在质能方程提出之后才有的，也就是说质速关系式是质能方程的推论。
你没看错，质速关系式是质能方程的推论！

所以从质速关系式开始推导质能方程的方法都是在循环论证。很多人把注意力都放在了推导过程中的微积分上面，根本就没有考虑前提条件合不合理。
动量四矢量
在这里要具体谈一谈上面挖的坑了：

为什么用动量守恒推导不出质速关系式？

注意，上面说的动量守恒指的是经典力学中的动量守恒。当然，这也是很正常的事，因为相对论力学已经包含了质能方程，如果用相对论力学中的“动量守恒”去推导，又是循环论证。
动不动就是循环论证，从零开始推导的难度可想而知。这也是爱因斯坦在1905年就提出“质能等价”的思想，却在1907年的论文里才写出严格推导过程的原因。

经典力学的动量守恒和相对论力学的动量守恒的最大区别就是：

经典力学中的动量守恒和能量守恒是独立的，考虑动量守恒的时候可以不考虑能量守恒。
相对论力学中的动量守恒和能量守恒是相互关联的，考虑动量守恒的时候必须考虑能量守恒。

相对论是用“四维的语言”书写的，就像三个空间维度和一个时间维度组成“四维时空”一样，动量和能量组成了“动量四矢量” 。

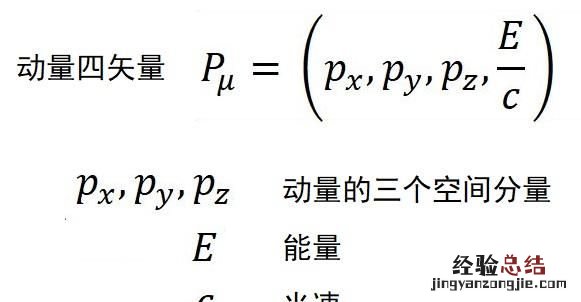
参考系改变时，动量四矢量也会改变，不同参考系中的动量四矢量之间的变换是洛伦兹变换。
就像下图展示的一样，新的参考系中的动量与旧的参考系中的能量有关，新的参考系中的能量也与旧的参考系中的动量有关。

也就是说，在不同参考系中考虑动量守恒的时候，也一定要把能量守恒考虑进去。
所以用经典力学的方法，单纯考虑不同参考系中的动量守恒根本就推导不出质速关系式。
写在最后
质能方程并不是一个可以轻易推导出来的公式。在物理学中，很多知识都是没法速成的，你以为的捷径，往往是陷阱。
凡事还是要脚踏实地，尤其是对待物理学。

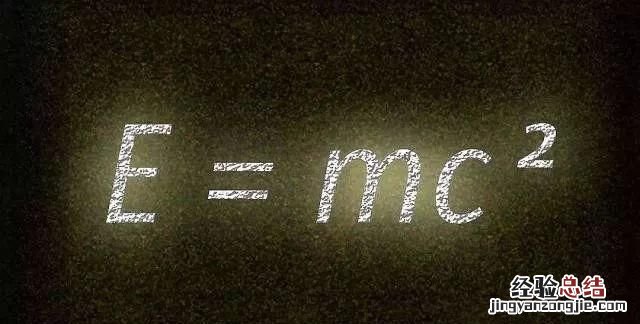
爱因斯坦质能方程的推导应该不会太难，一般的高中生都可以推导。
动能公式E=1/2mV平方
E是能量，m是质量，V是速度。
如果物体运动速度是光速C ，那么物体动能就是：
E=1/2mC平方
爱因斯坦质能公式：E=mC平方
E是能量，m是质量，C是光的速度。
如果把上面的动能公式与质能进行比较，就会发现两个公式很相似，它们之间的区别就是动能公式中的能量刚好是质能公式中的能量的1/2 。
上面的问题是什么原因造成的呢？可以肯定动能公式没有问题，这已经被证实的公式。问题就在质能公式中，因为所谓的质能方程没有理论依据，基本上是想象出来的，由于爱因斯坦自以为了不起自以为是，所以给我们忽悠出来了质能方程E=mC平方，这应该根本没有实际应用价值。
【质能方程，爱因斯坦质能方程的详细推导】
从理论推导如果质量真的可以转化成能量，那么根本不需要所谓的质能公式：E=mC平方，用动能公式：E1/2mV平方（这里的速度V换光速C）就可以了。从理论推导如果质量真的可以转化成能量，这应该与光速不存在直接关系，所以爱因斯坦的质能公式应该是谬论。