1)算法执行的时间可以反映出算法的效率么?
有编程经验的朋友经常会发现 , 对于同样一个问题,使用不同的算法实现 , 每种算法执行的时间可能是不同的 。比如不同的排序算法,运行时间上就有差异 。
但是,我们靠程序运行时间去衡量算法的优劣可靠么?同一个程序如果你放到一台古董机里跑的话,运行时间必然会更长 。所以凭借程序运行的时间来衡量算法的优劣势不准确的 。因为计算机的硬件配置和操作环境等客观因素会影响程序运行的速度,进而反应在程序运行的时间上 。
2)怎样客观地评价一个算法优劣呢?
我们假设计算机执行算法的每一个基本操作所用的时间是固定的 , 那么一个算法有多少执行步骤 , 乘以每一步骤需要花费的时间,就是程序运行的总时间 。对于不同的计算机而言,程序运行总时间的不尽相同的,但同一个算法程序执行的基本步骤是相同的,因此我们可以通过算法包含的基本操作个数去衡量算法的效率,也就是算法的时间复杂度 。
3)算法时间复杂度的理解
理论上,我们应该度算法进行详细具体的分析 。但在实践中,这种做法的价值却很有限 。对于算法的时间、空间性质 , 最重要的了解他的数量级和趋势 。举例来说 , 可以认为3n^2和100n^2属于同一个数量级,我们认为它们的效率“差不多”,都为n^2级 。
算法的时间复杂度有三种,分别是:
· 最优时间复杂度:算法完成工作最少需要多少基本操作;
· 最坏时间复杂度:算法完成工作最多需要多少基本操作;
· 平均时间复杂度:算法完成工作平均需要多少基本操作 。
下表中列举了不同基本操作步骤的情况下,时间复杂度的结果:
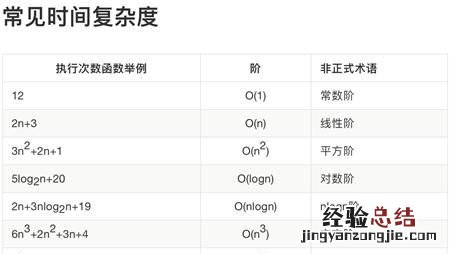
简单理解:算法时间复杂度就是当变量等于n的时候,算法需要操作次数的量级 。
举几个例子:
- O(1):执行次数是一个常数,不管变量多大 , 执行次数是固定的 。
- O(n):执行次数为n次,比如有n个数字 , 寻找里面最小的数字是多少,那么就要全部查找一遍 。
- O(n2):最简单的举例,双重循环
for (j=1; j<=n; j++){
x++;
}
}
还有冒泡排序,对于n个变量的数组,位置需要交换n2次
- O(log2n):分治算法,从小到大排列了100个数字,你要找其中的一个,先从第50个开始找 , 比较大小后选择是找前50个还是后50个,类推 。

如果算法里面有两个循环,一个for循环时间复杂度是O(n),还有一个双重for循环时间复杂度是O(n2),那么这个算法整体的时间复杂度O(n+n2)=O(n2),就是最大的那个 。
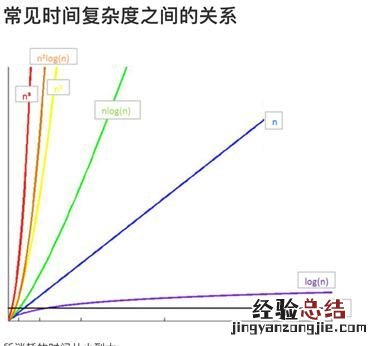
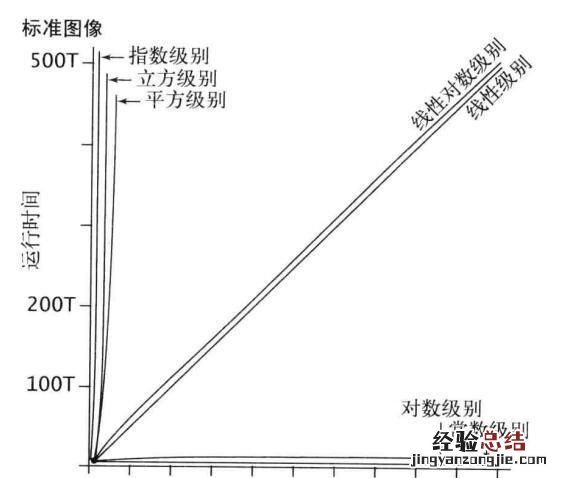
常见的算法时间复杂度由小到大依次为:
O(1)<O(log2n)<O(n)<O(nlog2n)<O(n2)<O(n3)<O(2^n)
【算法时间复杂度指的是什么】

希望我的解答可以帮助到你!
时间复杂度的表示: O(执行次数)
一个有序的元素列表查找某个元素可以用二分查找,每次取中间元素进行比较大小 , 直到相等 。因为每次不符合时总会排除一半的元素,所以查找的次数为log2n,那么时间复杂度为O(log2n) 。如果是一个无序的元素列表,查找从位置0开始,那么简单查找的次数为n , 那么时间复杂度为O(n) 。
除此之外快速排序为O(n*log2n) , 选择排序为O(n*n) 。
旅行算法就是n个旅行地点,你可从某个地方出发到余下某下一个地点,走完所有地点 。从最开始时走有n个地点可以选择,接下来再走就有n-1个地点可以选择,这样直到只有一个地点可以选择 。那么所有你可走的路径就是一个阶乘 , 选择复杂度为O( n!) 。
关于数组和链表的操作 。先说数组,因为你有了元素的索引 , 可以随机访问,你就能快速找到这个元素 , 而且所有元素的读取都是一样的步骤,所以读取时间复杂度为O(1),数组的插入和删除的时间复杂度为O(n),因为要移动元素 。链表的特性是每个都存储了下一个元素的地址,只能顺序访问 。那么读取插入删除的时间复杂度分别是O(n)、O(1)、O(1) 。