
文章插图
反函数是函数中最基本的概念,对于一些反函数问题,只要充分理解反函数的概念,弄清原函数和反函数的定义域、值域之间的关系 , 了解互为反函数的图象间的关系,则可不必求出反函数的解析式便能迅速获解 。
例1
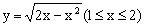
文章插图
的反函数是 。
A.
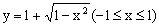
文章插图
B.
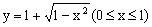
文章插图
C.

文章插图
D.
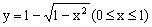
文章插图
解析:由

文章插图
,得
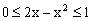
文章插图
,所以原函数的定义域为[1,2] , 值域为[0,1],则反函数的定义域为[0,1] , 值域为[1 , 2] 。通过观察四个选项 , 知答案为B 。
说明:利用互为反函数的两个函数的定义域、值域间的互换关系解题,可化繁为简,快速准确 。
例2 函数
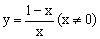
文章插图
的反函数的图象大致是

文章插图
A B C D
解析:由原函数不难得到反函数的定义域为
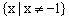
文章插图
,根据定义域可排除选项A、C , 又点(1,0)在原函数的图象上,所以点(0,1)在反函数的图象上 , 排除D,从而选B 。
说明:若函数

文章插图
的图象经过点(a,b),则它的反函数
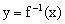
文章插图
的图象必过点(b,a),反之也成立 。利用这一结论,可避繁就简 , 轻松解题 。
例3 若函数
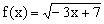
文章插图
,则
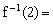
文章插图
_________ 。
解析:设
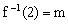
文章插图
【高等数学反函数的求法例题过程 反函数怎么求例题】,则
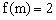
文章插图
,即
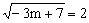
文章插图
, 解得
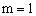
文章插图
,故
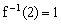
文章插图
。
说明:设函数的反函数为,则

文章插图
。本题巧妙利用这一结论,回避了求,解法简捷明快 。
例4 已知函数
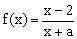
文章插图
的图象关于直线对称 , 求a的值 。
解析:因函数的图象关于直线对称,所以函数的定义域和值域相同 。又函数的定义域为
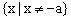
文章插图
,值域为

文章插图
,则
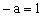
文章插图
, 即得
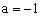
文章插图
。
说明:若函数的图象关于直线对称,则
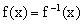
文章插图
,即的定义域和值域相同 。解题中若能适时运用这一结论,可达到事半功倍之效 。
例5 已知函数
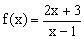
文章插图
, 若函数的图象与的图象关于直线对称,求
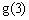
文章插图
的值 。
解析:由题设知函数是的反函数,设
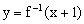
文章插图
,则

文章插图
,即
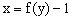
文章插图
,所以

文章插图
,可得
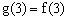
文章插图
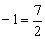
文章插图
。
说明:解决本题的常规思路是先由求,然后得,再求的反函数即,最后求的值 。这里运用互为反函数的两函数间的关系 , 在的两边同取“f”,减少运算避免错误 。但在解题时,我们常会有如下错解:先由得
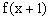
文章插图
,然后将的反函数误认为是来求解 。应引起同学们的注意 。
--END--












