运动和力的关系是怎样的?从远古至今天 , 人们一直在探寻着 。但从亚里士多德 “力是维持物体运动的原因”的观点,到牛顿第一定律告诉我们“力的真正效应不是使物体运动,而是改变物体的运动状态”,牛顿第二定律给出力和加速度的定量关系“F=ma”却经历了漫长的岁月 。从探究“马拉车前进的原因”,到现代研究“火车提速”、“嫦娥奔月”,人们从未停止过探索的脚步 。
文章插图
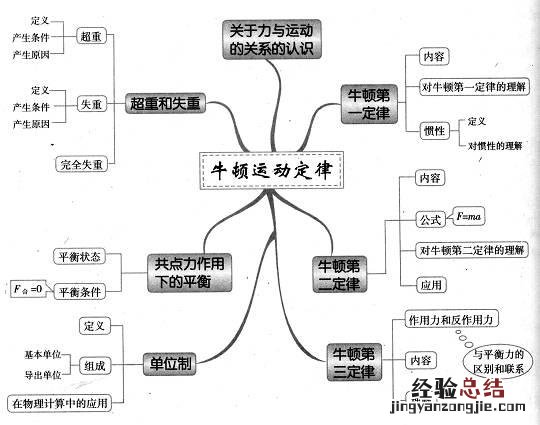
本讲探究牛顿第二定律在动力学问题中的应用 。
寻根溯源·根题展现 【根题】(人教版新课标必修1第90页例2)一个滑雪者 , 质量m=75kg , 以v0=2m/s的初速度沿山坡匀加速滑下,如图1甲所示,已知山坡的倾角θ=30°,在t=5s的时间内滑下的路程x=60m,且此时滑雪者刚好到达山坡底端 。g=10m/s2 。
(1)求滑雪者受到的阻力(包括摩擦和空气阻力) 。
(2)若滑雪者到达山坡底端后沿水平面继续滑行,此时所受阻力为其重力的0.2倍,求滑雪者沿水平面滑行的路程 。

文章插图

文章插图
【点评】本题是典型的动力学问题 , 代表了牛顿运动定律应用的两种基本类型 , 高考题中众多的斜面问题都可以从本题中找到解题的思路和方法 。
方法总结·规律提练 一、牛顿运动定律应用的两种基本类型
(1)已知物体的受力情况,求解物体的运动情况 。
解决这类题目,一般是应用牛顿运动定律求出物体的加速度,再根据物体的初始条件 , 应用运动学公式,求出物体运动的情况,即求出物体在任意时刻的位置、速度或运动时间等,流程图如下:

文章插图
(2)已知物体的运动情况,求解物体的受力情况 。
解决这类题目,一般是应用运动学公式求出物体的加速度,再应用牛顿第二定律求出物体所受的合外力 , 进而求出物体所受的其他外力 。流程图如下:

文章插图
这两种情况 , 力与运动间,均是以加速度为联系的桥梁 。
二、斜面上的常见受力情景图和相应的基本方程
牛顿第二定律作为力学的两大支柱之一 , 是高考考查的重点 , 无论在哪份试卷中都占有举足轻重的地位 。而物体在斜面上的受力分析又是重中之重 。下面以"斜面"为突破口,找到应用牛顿第二定律解题的密码 。

文章插图

文章插图

文章插图
考场精彩·衍题百变 一、斜面上的动力学问题 【衍题1】

文章插图

文章插图
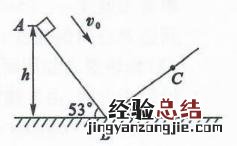
【衍题2】如图所示 , m=1.0kg的小滑块以v0=1m/s的初速度从倾角为53°的斜面AB的顶点A滑下,不计滑过B点时的机械能损失,BC段斜面倾角为37°,滑块与斜面间的动摩擦因数均为,A点离B点所在水平面的高度h=1.2m 。最大静摩擦力近似等于滑动摩擦力,取g=10m/s2,sin37°=0.6,cos37°=0.8 。
(1)求滑块到达B点时的速度大小 。
(2)从滑块到达B点时起,经0.6s正好通过C点,求BC之间的距离 。
文章插图

文章插图
【点拨】本题第(2)问出错率相当高,大都是未经分析而将题给的0.6s直接代入公式进行计算,犯了“硬套公式”的错误 。
二、动力学极值问题

文章插图

文章插图

文章插图
【点评】这道题的第(1)问考查运动学知识,不涉及牛顿运动定律,难度较?。坏灿胁簧偻挥凶邢干筇?nbsp;, 看到题目就对物体进行受力分析,试图应用牛顿运动定律求解加速度,结果走了弯路,浪费了时间 。第(2)问求解拉力F的最小值以及方向,对考生运用数学知识的能力要求较高 。从阅卷情况看,有相当多的考生虽然列出物理方程,却因无法求解而失分 。
三、巧用正交分解法,速解动力学问题 【衍题4】

文章插图

文章插图
【点评】应用正交分解法时 , 应当本着需要分解的力尽量少的原则来建立坐标系,比如斜面上的平衡问题,一般沿平行斜面和垂直斜面建立直角坐标系,这样斜面的支持力和摩擦力就落在坐标轴上,只需分解重力即可.当然,具体问题要具体分析 , 坐标系的选取不是一成不变的,要依据题目的具体情景和设问灵活选?。?
【总结】
以上四个题目,均是以斜面为情景的动力学问题,均是以“根题”为核心衍化而来的 。对于斜面上的动力学问题,做好“两分析”是关键,即受力分析和运动分析 。受力分析时画出受力图,运动分析时画出运动草图能起到“事半功倍”的效果 。
(1)正交分解法 。把某一个或多个矢量(如力、速度、加速度、位移等)沿两个相互垂直的坐标轴(x轴和y轴)进行分解 , 再在这两个坐标轴上列式求解.它是分析解决平衡问题、动力学问题、运动的合成与分解问题的基本方法.这里需要说明的是 , 正交分解法是一种纯粹的数学方法,建立坐标轴时可以不考虑力的实际作用效果.这也是此法与分解法的不同.分解的最终目的是为了合成(求某一方向的合力或总的合力).而合理恰当地建立坐标系可以简化解题过程,收到化繁为简的效果.
(2)用正交分解法求解牛顿定律问题的一般步骤:①受力分析,画出受力图,建立直角坐标系 , 确定正方向;②把各个力向x轴、y轴上投影;③分别在x轴和y轴上求各分力的代数和Fx、Fy;④沿两个坐标轴列方程Fx=max,Fy=may 。如果加速度恰好沿某一个坐标轴 , 则在另一个坐标轴上列出的是平衡方程 。
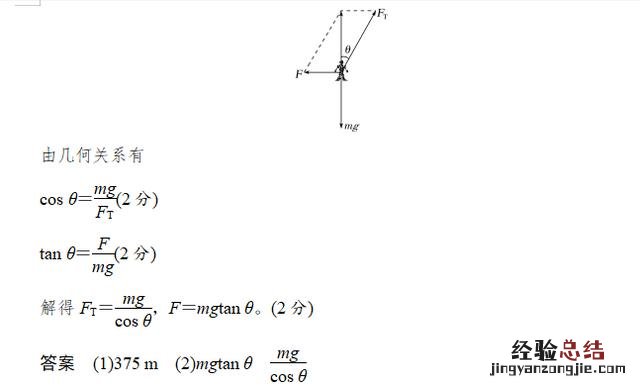
拓展延伸·纵横推演 一、“刚要分离”找临界 【衍题5】

文章插图
【点评】求解本题的关键是分析“相互接触的物体分离时的临界条件” 。相互接触的物体在刚好要分离时(也是恰好没有分离的状态)的条件包括两个方面 , 一是运动学条件,即两物体还有相同速度和相同加速度(本题中物体B和C刚要分离时,B的速度和加速度仍为零);二是动力学条件,即两个物体间弹力恰为零(假设弹力不为零,则两物体此时还“压”在一起,当然不会分离) , 抓住以上特点,即可顺利解题 。
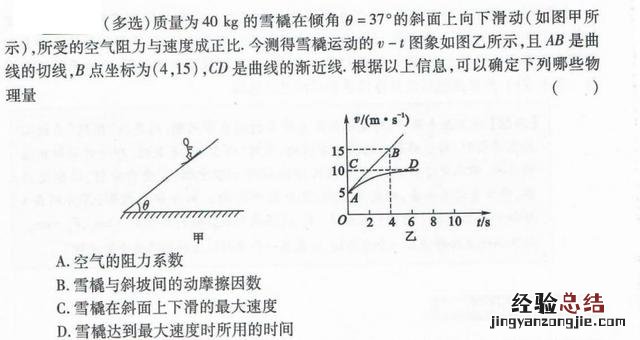
二、形象语言识图像 【衍题6】
文章插图

文章插图
【点评】解决本题的关键,先对雪橇进行受力分析,画出正确的受力图,然后由正交分解法列出牛顿第二定律的方程 。从物理图像上分别读取初、末两个状态的速度和加速度值 , 代入方程组便可确定能够求解的物理量 。
三、整体、隔离巧变换 【衍题7】

文章插图

文章插图
【衍题7】

文章插图

文章插图
【点评】对于有共同加速度的连接体问题 , 一般先用整体法由牛顿第二定律求出加速度,再根据题目要求,将其中的某个物体进行隔离分析并求解它们之间的相互作用力.将整体作为研究对象时 , 物体间的内力不能列入牛顿定律方程中,因为内力不影响整体的加速度 。
若一个系统内各个物体的加速度不相同 , 如本题中物块有加速度而斜面体没有加速度,整体法仍然适用 。这里依据的是力的独立作用原理 。需要特别注意的是“F=ma”中的质量m与研究对象的对应 。
【总结】
整体法和隔离法作为选择研究对象的基本能力,在动力学问题中得到了很好的体现 。整体法:在研究物理问题时,把所研究的对象作为一个整体来处理的方法称为整体法,采用整体法可以避免分析整体内部各物体之间的作用力 , 常常使受力简单明了 。隔离法:把所研究对象从整体中隔离出来进行分析,采用隔离物体法能使单个物体的受力特征突显出来 。
选取的原则:不涉及物体之间相互作用力时,采用整体法;涉及物体间相互作用力时采用隔离法 。
整体和局部是相对统一的 。一般问题的求解中 , 随着研究对象的转化,往往两种方法交叉运用,相辅相成 。所以,两种方法的取舍 , 并无绝对的界限,必须具体分析,灵活运用,无论哪种方法均以尽可能避免或减少非待求量(即中间未知量的出现 , 如非待求的力)的出现为原则 。
小试身手·根题精练

文章插图

文章插图

文章插图

文章插图

文章插图

文章插图

文章插图

文章插图
文章插图
【高中物理牛顿三大定律的知识梳理 高中物理牛顿运动定律公式总结】

文章插图