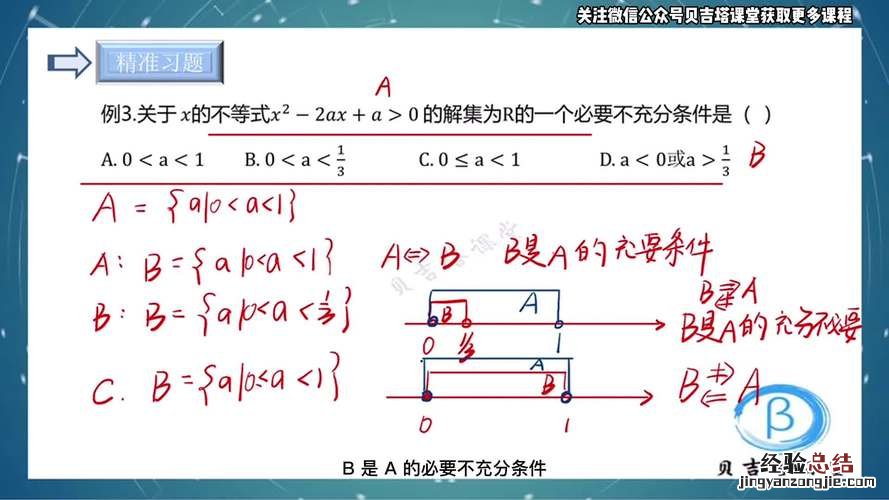
【充分条件和必要条件的口诀】当A能够推导出B时,可以说A是B的充分条件 。这意味着如果没有A,一定不会有B 。但是,如果有A,未必会有B , 这时A就是B的必要条件 。充分条件表明A是B的子集,也就是说属于A的一定属于B,但属于B的不一定属于A 。如果存在属于B但不属于A的元素 , 那么A就是B的真子集 。如果属于B的元素也属于A,那么A和B就相等 。必要条件是数学中一种关系形式 。如果没有A , 那么必然没有B 。如果有A,但不一定有B,那么A就是B的必要条件 , 可以表示为B→A,读作“B含于A” 。简单来说,如果从结果B可以推导出条件A , 那么我们可以说A是B的必要条件 。