经验总结

  1. 首页 > 生活 > >

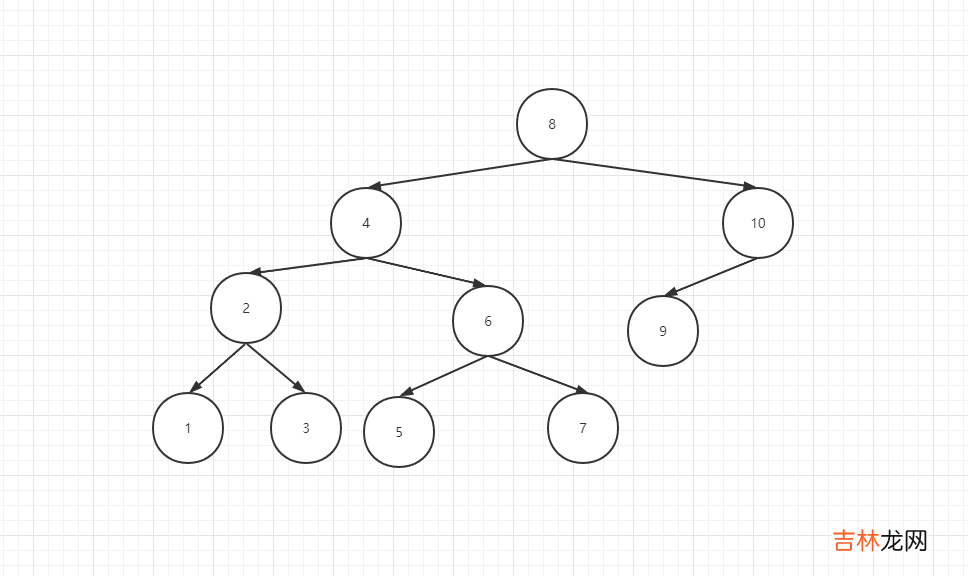
.Net CLR GC plan_phase二叉树和Brick_table( 二 )

生活百科

2.(if(true))：
3,5,7,9编号的node会进入这里，主要是设置右节点set_node_right_child (last_node, (new_node - last_node));3.(if(true))：
6,10编号的会进入这里，主要是把原来的二叉树的右子节点变成新的node(new_node)的左子节点，切断二叉树与它自己右子节点的联系 。然后把新的node(new_node）,变成原来二叉树的右子节点 。uint8_t*earlier_node = tree;size_t imax = logcount(sequence_number) - 2;//这里是获取需要变成的二叉树的右子树节点的层级 。for (size_t i = 0; i != imax; i++)//如果层级不等于0，则获取到二叉树根节点到右子节点的距离，然后把根节点与右子节点相加得到二叉树右子节点 。如此循环遍历，到二叉树最底层的右子节点为止 。{earlier_node = earlier_node + node_right_child (earlier_node);}获取到最后一颗二叉树的根节点的右子树的距离int tmp_offset = node_right_child (earlier_node);assert (tmp_offset); // should never be empty把最后一颗二叉树的根节点和最后一颗二叉树的右子节点相加，设置为新的node(new_node)的左子树 。set_node_left_child (new_node, ((earlier_node + tmp_offset ) - new_node));把最后一颗二叉树的右子树节点设置为新的node(new_node)节点，同时也是断了开与原来右子树的联系 。set_node_right_child (earlier_node, (new_node - earlier_node));GC plan_phase的二叉树构建本身并不复杂，而是复杂的逻辑和诡异的思维方式 。
最终的构建的二叉树形式如下图所示：

.Net CLR GC plan_phase二叉树和Brick_table

文章插图
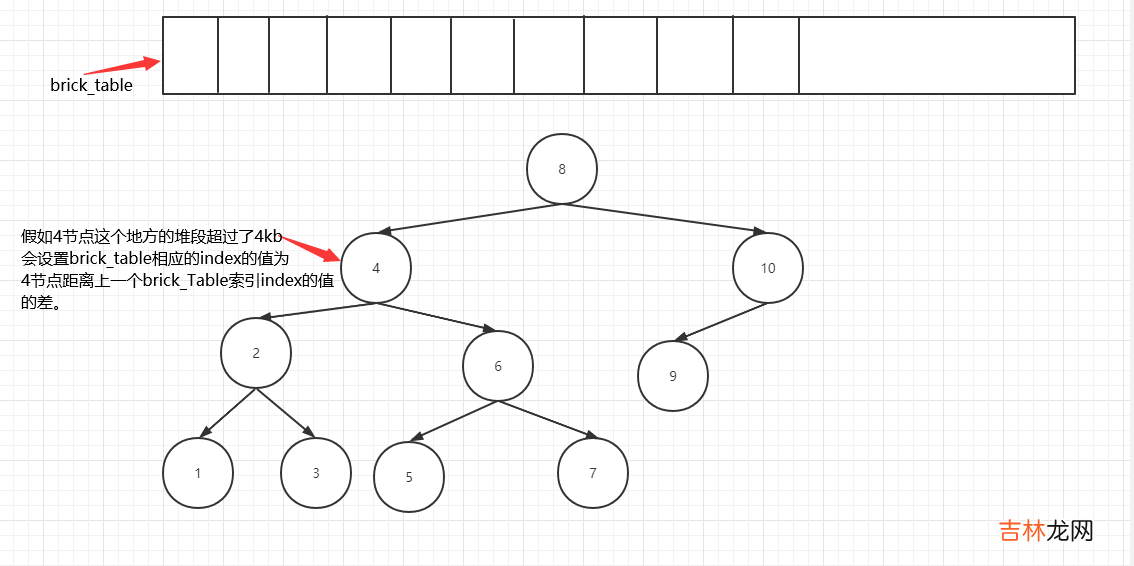
四.分割二叉树当以上二叉树被构建之后，如有几千个节点（node,小堆段）会形成庞大的一棵树 。所以需要分割功能，用以来保证性能 。
当二叉树包含的小堆段（node）的长度超过2的12次方（4kb），这棵二叉树就会被分割 。
.Net CLR GC plan_phase二叉树和Brick_table

文章插图
Brick_table里面属于这个4节点范围内的都是赋值为-1，表示你要在4节点上寻找你需要的节点 。
源码：最后上一下源码1.构建二叉树：
uint8_t* gc_heap::insert_node (uint8_t* new_node, size_t sequence_number,uint8_t* tree, uint8_t* last_node){dprintf (3, ("IN: %Ix(%Ix), T: %Ix(%Ix), L: %Ix(%Ix) [%Ix]",(size_t)new_node, brick_of(new_node),(size_t)tree, brick_of(tree),(size_t)last_node, brick_of(last_node),sequence_number));if (power_of_two_p (sequence_number)){set_node_left_child (new_node, (tree - new_node));dprintf (3, ("NT: %Ix, LC->%Ix", (size_t)new_node, (tree - new_node)));tree = new_node;}else{if (oddp (sequence_number)){set_node_right_child (last_node, (new_node - last_node));dprintf (3, ("%Ix RC->%Ix", last_node, (new_node - last_node)));}else{uint8_t*earlier_node = tree;size_t imax = logcount(sequence_number) - 2;for (size_t i = 0; i != imax; i++){earlier_node = earlier_node + node_right_child (earlier_node);}int tmp_offset = node_right_child (earlier_node);assert (tmp_offset); // should never be emptyset_node_left_child (new_node, ((earlier_node + tmp_offset ) - new_node));set_node_right_child (earlier_node, (new_node - earlier_node));dprintf (3, ("%Ix LC->%Ix, %Ix RC->%Ix",new_node, ((earlier_node + tmp_offset ) - new_node),earlier_node, (new_node - earlier_node)));}}return tree;}2.切割二叉树：
size_t gc_heap::update_brick_table (uint8_t* tree, size_t current_brick,uint8_t* x, uint8_t* plug_end){dprintf (3, ("tree: %Ix, current b: %Ix, x: %Ix, plug_end: %Ix",tree, current_brick, x, plug_end));if (tree != NULL){dprintf (3, ("b- %Ix->%Ix pointing to tree %Ix",current_brick, (size_t)(tree - brick_address (current_brick)), tree));set_brick (current_brick, (tree - brick_address (current_brick)));//brick_table索引处的值是：根节点tree距离当前current_brick对应的地址的距离}else{dprintf (3, ("b- %Ix->-1", current_brick));set_brick (current_brick, -1);}size_tb = 1 + current_brick;ptrdiff_toffset = 0;size_t last_br = brick_of (plug_end-1);//上一个plug节点的末尾current_brick = brick_of (x-1);//当前的plug_startdprintf (3, ("ubt: %Ix->%Ix]->%Ix]", b, last_br, current_brick));while (b <= current_brick){if (b <= last_br){set_brick (b, --offset);}else{set_brick (b,-1);}b++;}return brick_of (x);}

经验总结扩展阅读


上一篇：创维电视音量调不动

下一篇：晋升原因和理由怎么写