知识图谱实体对齐2:基于GNN嵌入的方法1 导引我们在上一篇博客《知识图谱实体对齐1:基于平移(translation)嵌入的方法》中介绍了如何对基于平移嵌入+对齐损失来完成知识图谱中的实体对齐 。这些方法都是通过两个平移嵌入模型来将知识图谱\(\mathcal{G}_1\)和\(\mathcal{G}_2\)的重叠实体分别进行嵌入,并加上一个对齐损失来完成对齐 。不过,除了基于平移的嵌入模型之外,是否还有其它方式呢?
答案是肯定的 。目前已经提出了许多基于GNN的实体对齐方法[1],这些方法不仅采用GNN捕捉更多的实体结构化信息,还通过诸如参数共享、参数交换等方式在embedding模块中就使实体的embeddings尽可能统一到一个向量空间 。
基于GNN的方法可以被分为基于GCN(graph convolutional network)的和基于GAT(graph attention network)两类,它们常常使用实体的邻居知识来对知识图谱的结构进行编码,大多数邻居及被做为嵌入模块的输入特征 。因为这里存在一个假定,即对齐的实体将有相似的邻居 。大多数基于GNN的方法在训练中只使用实体来做为对齐种子,而不是关系来做为对齐种子 。
2 基于GNN的方法2.1 GCN-Align本文是第一篇采用GNN来进行实体对齐的工作[2] 。GCN-Align使用两个GCN来将\(\mathcal{G}_1\)和\(\mathcal{G}_2\)的实体嵌入到一个统一的向量空间中(这两个GCN使用共享权重矩阵) 。
\[\boldsymbol{H}^{(l+1)}=\sigma\left(\hat{\boldsymbol{D}}^{-\frac{1}{2}} \hat{\boldsymbol{A}} \hat{\boldsymbol{D}}^{-\frac{1}{2}}\boldsymbol{H}^{(l)} \boldsymbol{W}^{(l)}\right)\](注:原论文除了实体embeddings,还还有个属性embedings,我们这里从简省略)这里\(\boldsymbol{H}^{(l+1)}\)是实体的embeddings,\(\boldsymbol{W}^{(l)}\)是其对应的权重,\(\hat{\boldsymbol{A}}=\boldsymbol{A}+\boldsymbol{I}\)意为带自环的权重矩阵,\(\hat{\boldsymbol{D}}\)意为\(\hat{\boldsymbol{A}}\)的节点度矩阵(用于归一化使用) 。
不过GCN-Align和GCN有所不同,GCN-Align在计算\(a\in \mathbb{A}\)时还考虑了不同的关系谓词 。新的邻接矩阵计算如下:
\[a_{i j} \in \boldsymbol{A}=\sum_{\left(e_i, r, e_j\right) \in \mathcal{T}} g_h(r)+\sum_{\left(e_j, r, e_i\right) \in \mathcal{T}} g_t(r)\]这里函数\(g_h(r)\)和\(g_t(r)\)计算了由关系\(r\)连接的头实体和尾实体的数目再除以含有关系\(r\)的实体数量 。\(\mathcal{T}\)为知识图谱中所有元组的集合 。\((e_j, r, e_i)\)和\((e_i, r, e_j)\)都是KG中的元组 。函数\(g_h(r)\)和\(g_t(r)\)分别计算关系\(r\)所连接的头实体和尾实体数量 。这样,邻接矩阵\(\boldsymbol{A}\)就有助于对embedding信息如何在实体间传递进行建模 。
然后,GCN-Align的训练也是由最小化间隔损失(参见我们上一篇博客《知识图谱实体对齐1:基于平移(translation)的方法》)来完成,其alignment score function定义为:
\[\begin{aligned} f_{\text {align }}\left(e_1, e_2\right)=& \frac{1}{d}\left.\| \boldsymbol{h}\left(e_1\right)-\boldsymbol{h}\left(e_2\right)\right) \|_{L_1} \end{aligned}\]这里\(h(\cdot)\)表示维度为\(d\)的实体嵌入 。
整个网络的架构如下:
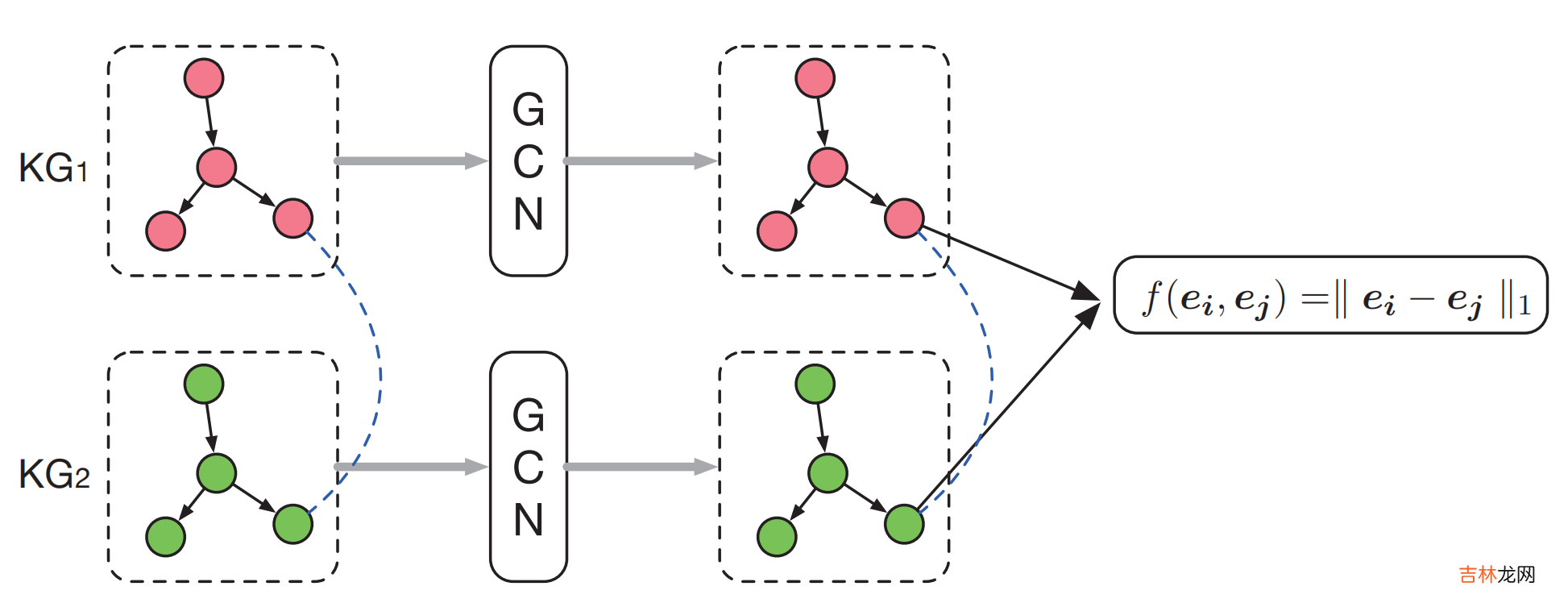
文章插图
2.2 HGCNHGCN[3]在实体嵌入的过程中隐式地利用关系的表示来改善对齐过程 。为了包含关系信息,HGCN同时学习实体和关系谓词的embeddings,
其整个包含embedding和align模块的框架如下:
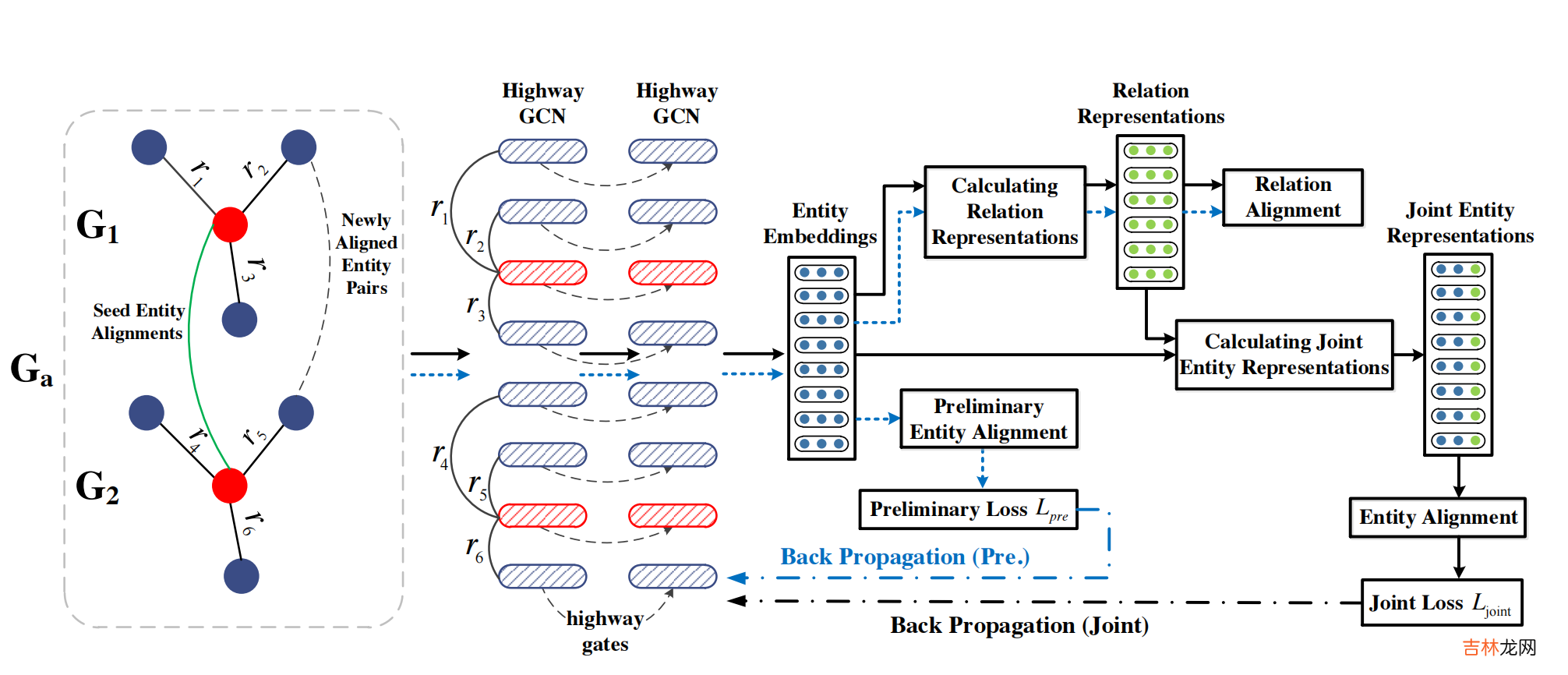
文章插图
本文提出的框架可分为以下的三个阶段:
Stage 1使用GCN的变种Highway-GCN来将实体嵌入到统一的向量空间 。这里直接将\(\mathcal{G}_1\)和\(\mathcal{G}_2\)视作一个图\(G_a\),然后使用一个统一的GCN来获得\(G_a\)的实体嵌入:
经验总结扩展阅读
- 关于立秋的知识
- 夏季极端天气预防知识
- 防中暑安全知识
- 高温天气行车安全知识
- 关于垃圾分类的知识
- springboot 多线程的使用
- 2023三伏天养生时间表 三伏天养生知识
- 蝉的科普知识
- 怎样学习电脑知识
- 关于电容器的高中相关知识















