知识图谱实体对齐2：基于GNN嵌入的方法( 二 ) _生活百科

\[\boldsymbol{H}^{(l+1)}=\operatorname{ReLU}\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} \boldsymbol{X}^{(l)} \boldsymbol{W}^{(l)}\right)\]我们这里采用逐层的highway gates（高速门）来建立Highway-GCN(HGCN)模型。逐层的highway gates用于控制GCN网络中的前向传播，写为以下的函数\(T\)的形式：
\[T\left(\boldsymbol{H}^{(l)}\right)=\sigma\left(\boldsymbol{H}^{(l)} \boldsymbol{W}^{(l)}+\boldsymbol{b}^{(l)}\right)\\\boldsymbol{H}^{(l+1)}=T\left(\boldsymbol{H}^{(l)}\right) \odot \boldsymbol{H}^{(l+1)}+\left(\mathbf{1}-T\left(\boldsymbol{H}^{(l)}\right)\right) \odot \boldsymbol{H}^{(l)}\]这里\(\boldsymbol{H}^{(l)}\)是\(l^{th}\)层的输出，\((l+1)^{th}\)层的输入。\(\odot\)是逐元素乘。
这样，HGCN分别计算两个KG的embeddings，并在训练中仍然使用上面所提到过的的alignment score function \(f_{\text{align}}(e_1, e_2)\)+间隔损失函数。
Stage 2基于关系谓词的头实体和尾实体的表征来获得其embeddings 。该阶段先分别计算所有连接关系谓词的头实体和尾实体的平均embeddings，接着这两个均值embeddings会在一个线性变换之后拼接起来做为关系的embeddings，这样就可以对跨知识图谱的关系进行对齐。
Stage 3再次使用Highway-GCN（其输入为Stage 1中得到的embeddings和与该实体有关的关系谓词embeddings之和的拼接）做为共同的实体embeddings，然后alignment模块再次使用alignment score function + 间隔损失将两个知识图谱在Highway-GCN的输出映射到统一的向量空间。
2.3 GMNNGMNN[4]将实体对齐问题形式化了为两个图之间做匹配的问题。传统的图匹配问题会通过对单语言知识图谱的事实进行编码，将每个知识图谱的实体投影到低维子空间。然而，对于跨语言问题，一些实体在不同的语言中可能存在不同的知识图谱事实，这可能导致其在在跨语言的实体embeddings中编码的信息具有差异性，从而使得这类方法难以对实体进行匹配。

文章插图
如上图展示了我们对\(e_0\)和\(e_0'\)进行对齐的实例。但是在它们周围的邻居中只有一个对齐的邻居。这种方法得匹配只有很少的邻居的实体非常困难，因为缺乏足够的结构化信息。
为了解决这个缺点，作者提出了topic entity graph（主题实体图）来表征知识图谱中实体的上下文信息。不同于之前的方法使用实体embeddings来匹配实体，作者将这个任务建模为在topic entity graph之间进行图匹配。每个实体都对应一个topic entity graph（由相隔一跳的邻居和对应的关系谓词组成），这样的一个图能够表征实体的局部上下文信息。
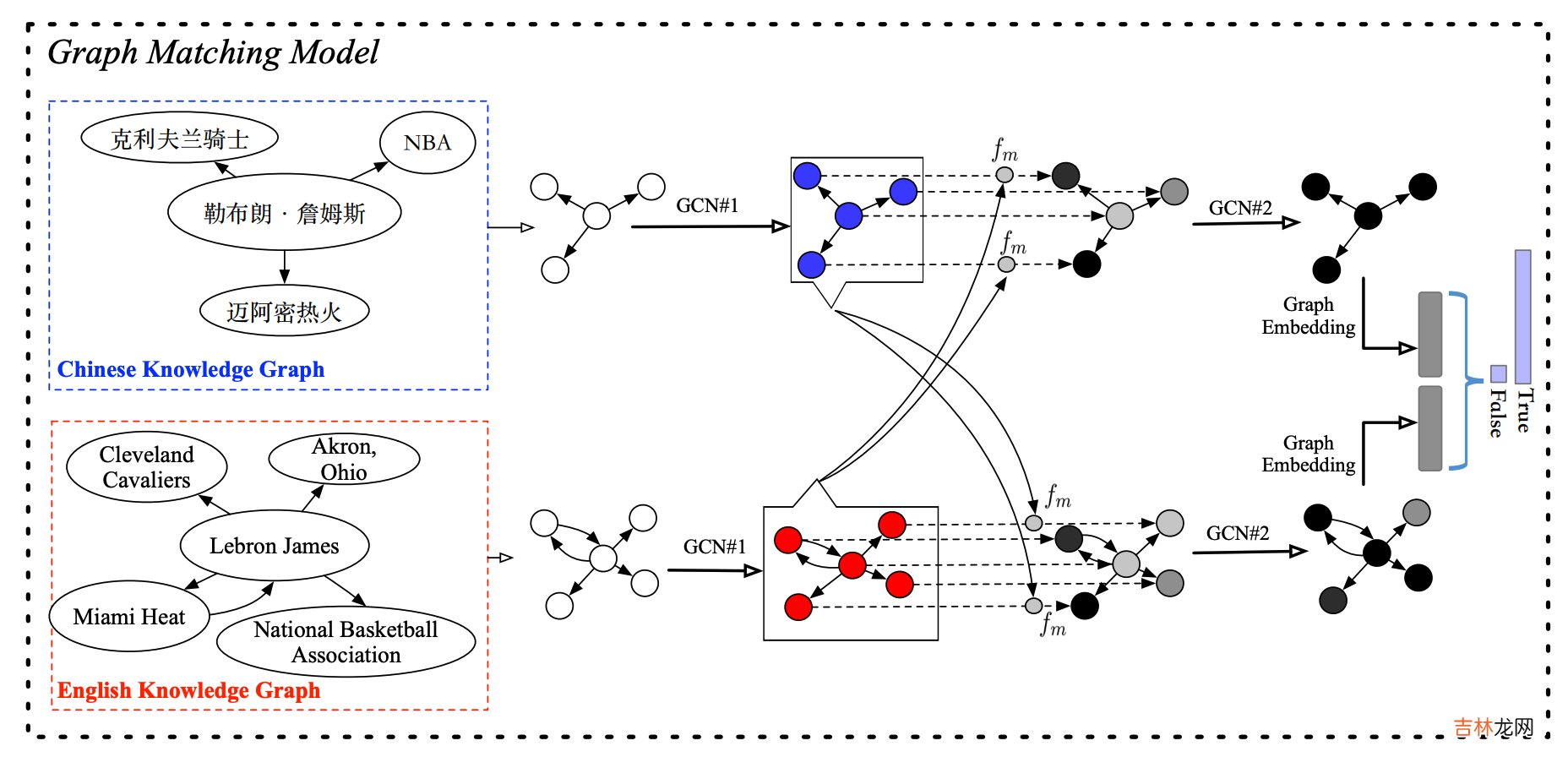
该论文提出的由四层组成，包括输入表示层、node-level匹配层，graph-level匹配层和预测层。如下图所示：

文章插图
输入表示层使用GCN将两个topic graph进行编码并获得实体的embeddings 。
【知识图谱实体对齐2：基于GNN嵌入的方法】node-level匹配层计算来自两个topic graph的实体对之间的余弦相似度。之后，这一层会计算实体embeddings的注意力加权和(attentive sum)：
\[\overline{\boldsymbol{e}}_i=\frac{\sum_{j=1}^{\left|\mathcal{E}_2\right|} \alpha_{i, j} \cdot \boldsymbol{e}_j}{\sum_{j=1}^{\left|\mathcal{E}_2\right|} \alpha_{i, j}}\]这里\(\alpha_{i,j}\)是某个topic graph中的实体\(i\)和另一个topic graph中的实体\(j\)之间的余弦相似度。接着，我们使用multi-perspective sine matching function\(f_m\)来计算\(\mathcal{G}_1\)和\(\mathcal{G}_2\)所有实体的匹配向量，如下式所示：