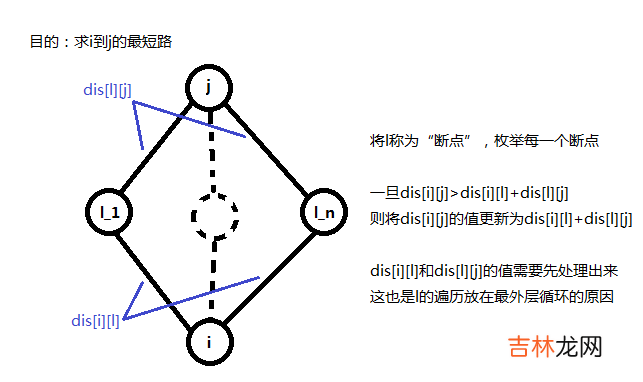
Autobus 方法记录( 二 ) _生活百科

若\(dis[i][j]\)是由\(dis[i][l]+dis[l][j]\)更新而来的，那么在这种情况下\(i\)到\(j\)的经过边数就是\(i\)到\(l\)的经过边数与\(l\)到\(j\)的经过边数的总和。

文章插图
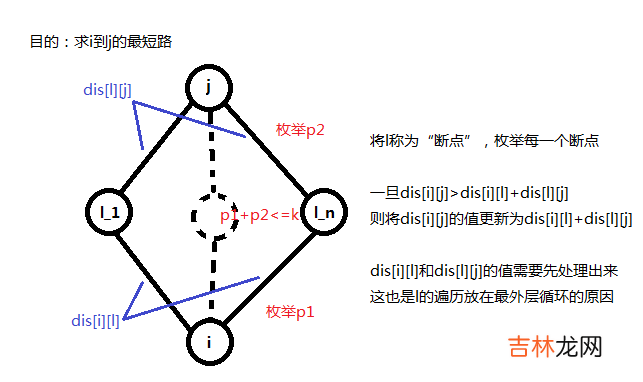
那\(i\)到\(j\)可能的经过的边数就可以通过\(i\)到\(l\)与\(l\)到\(j\)可能经过的边数更新。我们的方法是，外层循环从\(1\)到\(k\)枚举\(i\)到\(l\)可能经过的边数\(p1\)，内层循环从\(1\)枚举\(l\)到\(j\)可能经过的边数\(p2\)，且\(p1+p2<=k\).

文章插图

k=minn(k,n);for(int l=1;l<=n;l++)//l枚举断点{	for(int i=1;i<=n;i++)	{for(int j=1;j<=n;j++)//floyd标志性的三层for循环{for(int p1=1;p1<=k;p1++)//i到l可能的边数{for(int p2=1;p2<=k&&p1+p2<=k;p2++)//l到j可能的边数{dis[i][j][p1+p2]=minn(dis[i][j][p1+p2],dis[i][l][p1]+dis[l][j][p2]);}}}	}}

然后我们便得到了从点\(i\)到点\(j\)，经过\(1~k\)条边的最短路。然后我们再用\(ans[i][j]\)处理出这经过\(1~k\)条边的方案中最短的情况。（即最短路中的最短路）
综合以上两种情况，\(ans[i][j]\)就是最终的最短路了。
如果想用以下代码AC，需要做好常数优化，比如\(O2\),\(register\)...

#include<iostream>#include<cstdio>#include<cstring>#include<algorithm>using namespace std;const int inf=1e9;const int N=75;int n,m,a,b,t;int k,q,c,d;int dis[N][N][N];//dis[i][j][k]:经过k条边的前提下，i到j的最短路int ans[N][N];int minn(int a,int b){	return a<b?a:b;}int main(){	scanf("%d%d",&n,&m);	for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)for(int k=1;k<=n;k++)dis[i][j][k]=1e9;	for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)ans[i][j]=1e9;	for(int i=1;i<=n;i++)for(int k=1;k<=n;k++)dis[i][i][k]=0;	for(int i=1;i<=n;i++)ans[i][i]=0;	for(int i=1;i<=m;i++)	{scanf("%d%d%d",&a,&b,&t);dis[a][b][1]=minn(dis[a][b][1],t);ans[a][b]=minn(ans[a][b],t);	}	scanf("%d%d",&k,&q);	if(k>=n)	{for(int l=1;l<=n;l++)//l枚举断点{for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)//floyed标志性的三层for循环{ans[i][j]=minn(ans[i][j],ans[i][l]+ans[l][j]);//ans[i][j]根据floyed算法的定义，为i到j的最短路}}}	}	else	{k=minn(k,n);for(int l=1;l<=n;l++)//l枚举断点{for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)//floyed标志性的三层for循环{for(int p1=1;p1<=k;p1++)//i到l可能的边数{for(int p2=1;p2<=k&&p1+p2<=k;p2++)//l到j可能的边数{dis[i][j][p1+p2]=minn(dis[i][j][p1+p2],dis[i][l][p1]+dis[l][j][p2]);}}}}}for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)ans[i][j]=inf;for(int i=1;i<=n;i++)for(int j=1;j<=n;j++)for(int l=1;l<=k;l++)ans[i][j]=minn(ans[i][j],dis[i][j][k]);	}	for(int i=1;i<=q;i++)	{scanf("%d%d",&c,&d);if(c==d) puts("0");else if(ans[c][d]==inf) puts("-1");else printf("%d\n",ans[c][d]);	}	return 0;}

继续考虑，若我们能优化掉一层循环，是不是就可以更安稳地A掉这道题了？
依然是以\(k\)作为突破口，有以下策略：“\(k\)越大，答案一定不会更差。”现在我们要利用这种策略，那么上文“令\(dis[i][j][k]\)表示经过\(k\)条边的前提下，\(i\)到\(j\)的最短路”的定义就不合适了。因为我们并不一定要把\(k\)条边走完，\(k\)只是我们做选择时的限制。\(k\)越大，说明限制越宽松。
那么我们的解法便初具雏形了。最外层从\(2\)到\(k\)枚举每一种最大经过的边限制，（为什么不从\(1\)开始枚举？因为最多经过一条边就是相邻两点间的距离了）在循环内跑一个\(floyd\)，总共四层循环。
剩下的问题就是，转移方程如何设计。首先我们需要明确一点：\(k\)越大，说明选择的面更广，所以每一次的答案，是从上一次的答案加上“新的选择”生成的。