原题链接
[COCI2021-2022#4] Autobus题目描述在一个国家里有 \(n\) 座城市 。这些城市由 \(m\) 条公交线路连接,其中第 \(i\) 条线路从城市 \(a_i\) 出发,到 \(b_i\) 停止,路程中耗时 \(t_i\) 分钟 。
Ema 喜欢旅行,但她并不喜欢在公交线路之间换乘 。在旅行过程中,她希望最多只需坐 \(k\) 个不同的公交线路 。
Ema 想知道,从城市 \(c_i\) 到城市 \(d_i\) 的最短旅行时间是多少(最多坐 \(k\) 个不同的公交线路) 。
输入格式第一行包含两个整数 \(n,m\),分别表示城市的数量和公交车线路的数量 。
接下来 \(m\) 行,第 \(i+1\) 包含三个整数 \(a_i,b_i,t_i\),分别表示第 \(i\) 条公交车线路的起点、终点和从起点到终点所需的时间 。
接下来一行包含两个整数 \(k,q\),最大坐的不同公交线路的个数和问题题的个数 。
接下来 \(q\) 行,第 \(m+j+3\) 行包含两个整数 \(c_j,d_j\),表示询问从城市 \(c_j\) 到城市 \(d_j\) 的最短旅行时间 。
输出格式输出包含 \(q\) 行,第 \(i\) 行包含一个整数,表示从城市 \(c_i\) 到城市 \(d_i\) 的最短旅行时间 。
样例 #1样例输入 #14 71 2 11 4 102 3 12 4 53 2 23 4 14 3 21 31 44 23 3样例输出 #110-10样例 #2样例输入 #24 71 2 11 4 102 3 12 4 53 2 23 4 14 3 22 31 44 23 3样例输出 #2640样例 #3样例输入 #34 71 2 11 4 102 3 12 4 53 2 23 4 14 3 23 31 44 23 3样例输出 #3340提示【样例解释】
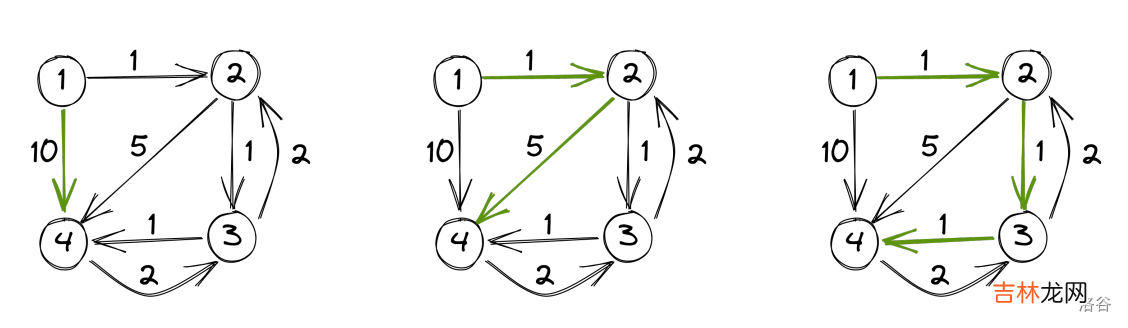
文章插图
每个样例中的答案都已经标记在图中 。
【数据规模与约定】
本题采用子任务捆绑测试 。
- Subtask 1(15 pts):\(k ≤ n ≤ 7\) 。
- Subtask 2(15 pts):\(k ≤ 3\) 。
- Subtask 3(25 pts):\(k ≤ n\) 。
- Subtask 4(15 pts):没有额外限制 。
【提示与说明】
本题分值按 COCI 原题设置,满分 \(70\) 。
题目译自 COCI2021-2022 CONTEST #4 T2Autobus 。
题解题目的要求是求全源最短路,而且\(n\)(图上总点数)非常小,和\(floyd\)的相性很好,所以首先考虑\(floyd\)算法 。
本题的第一个难点在于“最多只需坐\(k\)个不同的公交线路” 。但仔细观察数据范围,\(2\le n \le 70,1\le k \le10^9\),可以见得在大部分情况下,\(k\)是比\(n\)大的 。因为每个点至多到一次,所以一个点到该定点的线路也最多走一次,最复杂的旅行方案也只需要走\((n-1)\)条线路 。而\(k\)比\(n\)大就意味着旅行不再受“最多只需坐\(k\)个不同的公交线路”的限制 。
所以,对于这部分的数据,我们可以跑一个裸的\(floyed\)来处理出图上任意两个点之间的最短路 。
if(k>=n){ for(int l=1;l<=n;l++)//l枚举断点 {for(int i=1;i<=n;i++){for(int j=1;j<=n;j++)//floyd标志性的三层for循环{ans[i][j]=minn(ans[i][j],ans[i][l]+ans[l][j]);//ans[i][j]根据floyd算法的定义,为i到j的最短路}} }}那么剩下的问题就是处理会受\(k\)值限制的情况了 。既然有一个对经过路径条数限制的条件,那么我们不妨给记录最短路的数组再增加一个维度 。
令\(dis[i][j][k]\)表示经过\(k\)条边的前提下,\(i\)到\(j\)的最短路 。再加入\(k\)限制之前,我们先来看看传统的\(floyd\)是如何工作的 。
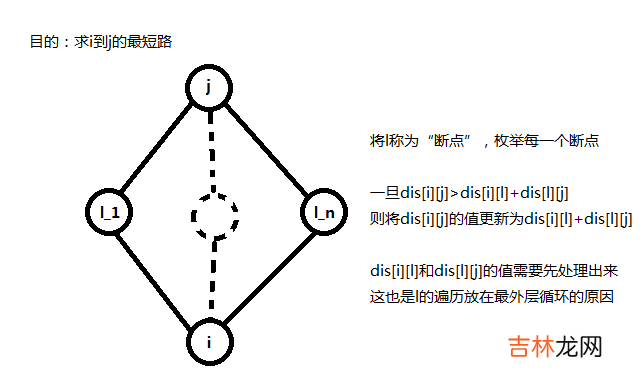
文章插图
可以直观地看到,类似动态规划,\(dis[i][j]\)可能由\(dis[i][l]+dis[l][j]\)更新而来,或者由\(dis[i][j]\)直接继承 。
那么考虑在这个更新的过程中加入\(k\)的限制 。
经验总结扩展阅读
- 11岁孩子犯错处罚方法
- 竹制品怎样防虫防霉
- ph试纸的正确使用方法
- 元气骑士战利品箱子获取方法
- 苏子叶冷冻保存方法
- 夏天冰糖的保存方法
- 三星手机截屏怎么操作方法(三星敲击截图)
- 金属除锈最简单的方法
- 盗钥匙的方法香川照之演的是啥角色?
- 2022年实时最新省市区县乡镇街道geojson行政边界数据获取方法














