在第四行,(5,5,5)情形下的矩阵乘法,AlphaTensor计算出来的方法可以在博客里面看到,非常复杂,为了减少两次乘法,却耗费了数几十次加法 。因此AlphaTensor只能做到渐进时间复杂度更优,在大矩阵情形下达到更快的速度 。
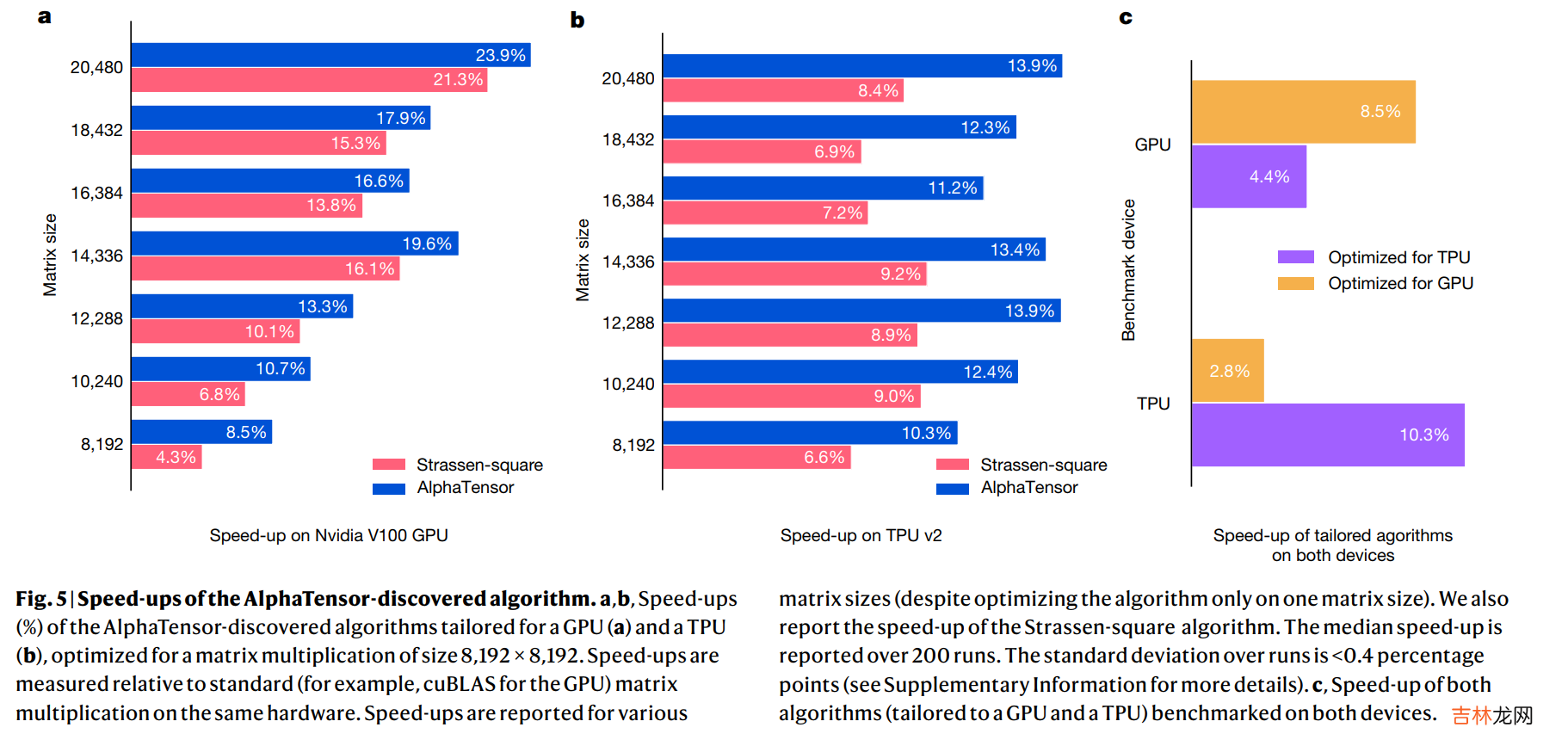
值得关注的是,他们在\(8192*8192\)的方阵乘法上进行了测试,采用\(4*4\)分块的方式(这样每个子矩阵的大小就是\(2048*2048\)规模的了),AlphaTensor方法比Strassen的方法减少了两次矩阵乘法,因此加速比从1.043提升至1.085 。这说明这一方法相比coppersmith-winograd方法(\(O(n^{2.37})\))那种银河算法更加实用,常数更低,在8192规模的矩阵就能生效了 。而且,计算矩阵乘法的Algorithm 1也方便在GPU和TPU上并行 。
文章插图
经验总结扩展阅读
- GGD 论文解读《Rethinking and Scaling Up Graph Contrastive Learning: An Extremely Efficient Approach with Group Discrimination》
- AlexNet-文献阅读笔记
- 图书馆的超星阅览室怎么免费下载电子书 超星校园阅读系统
- CVPR2022 Oral OGM-GE阅读笔记
- 带你读AI论文丨ACGAN-动漫头像生成
- Java核心技术阅读笔记 java中的自动拆装箱与缓存
- pdf阅读器如何进行页面裁剪
- 英语论文答辩技巧
- 从SpringBoot启动,阅读源码设计
- 【论文翻译】KLMo: Knowledge Graph Enhanced Pretrained Language Model with Fine-Grained Relationships









