GGD 论文解读《Rethinking and Scaling Up Graph Contrastive Learning: An Extremely Efficient Approach with Group Discrimination》 _生活百科

论文信息

论文标题：Rethinking and Scaling Up Graph Contrastive Learning: An Extremely Efficient Approach with Group Discrimination论文作者：Yizhen Zheng, Shirui Pan, Vincent Cs Lee, Yu Zheng, Philip S. Yu论文来源：2022，NeurIPS论文地址：download 论文代码：download

1 IntroductionGCL 需要大量的 Epoch 在数据集上训练，本文的启发来自 GCL 的代表性工作 DGI 和 MVGRL，因为 Sigmoid 函数存在的缺陷，因此，本文提出 Group Discrimination (GD) ，并基于此提出本文的模型 Graph Group Discrimination (GGD) 。
Graph ContrastiveLearning 和 Group Discrimination 的区别：

GGD 论文解读《Rethinking and Scaling Up Graph Contrastive Learning: An Extremely Efficient Approach with Group Discrimination》

文章插图

GD directly discriminates a group of positive nodes from a group of negative nodes.
GCL maximise the mutual information (MI) between an anchor node and its positive counterparts, sharing similar semantic information while doing the opposite for negative counterparts.

贡献：

1) We re-examine existing GCL approaches (e.g., DGI and MVGRL), and we introduce a novel and efficient self-supervised GRL paradigm, namely, Group Discrimination (GD).
2) Based on GD, we propose a new self-supervised GRL model, GGD, which is fast in training and convergence, and possess high scalability.
3) We conduct extensive experiments on eight datasets, including an extremely large dataset, ogbn-papers100M with billion edges.

2 Rethinking Representative GCL Methods本节以经典的 DGI 、MVGRL 为例子，说明了互信息最大化并不是对比学习的贡献因素，而是一个新的范式，群体歧视（group discrimination）。
2.1 Rethinking GCL Methods回顾一下 DGI ：

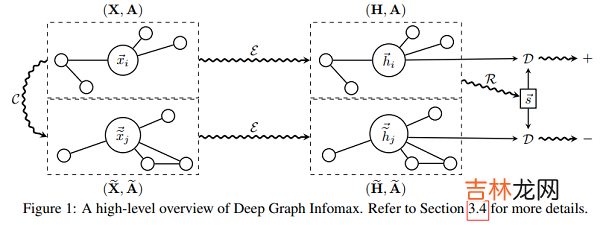
文章插图
代码：

文章插图

文章插图
class DGI(nn.Module):def __init__(self, g, in_feats, n_hidden, n_layers, activation, dropout):super(DGI, self).__init__()self.encoder = Encoder(g, in_feats, n_hidden, n_layers, activation, dropout)self.discriminator = Discriminator(n_hidden)self.loss = nn.BCEWithLogitsLoss()def forward(self, features):positive = self.encoder(features, corrupt=False)negative = self.encoder(features, corrupt=True)summary = torch.sigmoid(positive.mean(dim=0))positive = self.discriminator(positive, summary)negative = self.discriminator(negative, summary)l1 = self.loss(positive, torch.ones_like(positive))l2 = self.loss(negative, torch.zeros_like(negative))return l1 + l2本文研究 DGI 结论：一个 Sigmoid 函数不适用于权重被 Xavier 初始化的 GNN 生成的 summary vector，且 summary vector 中的元素非常接近于相同的值。
接着尝试将 Summary vector 中的数值变换成不同的常量（from 0 to 1）：
【GGD 论文解读《Rethinking and Scaling Up Graph Contrastive Learning: An Extremely Efficient Approach with Group Discrimination》】

文章插图
结论：

- 将 summary vector 中的数值变成 0，求解相似度时导致所有的 score 变成 0，也就是 postive 项的损失函数变成负无穷，无法优化；
- summary vector 设置其他值，导致数值不稳定；

DGI 的简化：
① 将 summary vector 设置为单位向量（缩放对损失不影响）；
② 去掉 Discriminator （Bilinear? ：先做线性变换，再求内积相似度）的权重向量；【双线性层的 $W$ 其实就是一个线性变换层】
$\begin{aligned}\mathcal{L}_{D G I} &=\frac{1}{2 N}\left(\sum\limits _{i=1}^{N} \log \mathcal{D}\left(\mathbf{h}_{i}, \mathbf{s}\right)+\log \left(1-\mathcal{D}\left(\tilde{\mathbf{h}}_{i}, \mathbf{s}\right)\right)\right) \\&\left.=\frac{1}{2 N}\left(\sum\limits_{i=1}^{N} \log \left(\mathbf{h}_{i} \cdot \mathbf{s}\right)+\log \left(1-\tilde{\mathbf{h}}_{i} \cdot \mathbf{s}\right)\right)\right) \\&=\frac{1}{2 N}\left(\sum\limits_{i=1}^{N} \log \left(\operatorname{sum}\left(\mathbf{h}_{i}\right)\right)+\log \left(1-\operatorname{sum}\left(\tilde{\mathbf{h}}_{i}\right)\right)\right)\end{aligned} \quad\quad\quad(1)$