OpenMP 入门( 二 ) _生活百科

parallel region 1 thread id = 0parallel region 1 thread id = 3parallel region 1 thread id = 1parallel region 1 thread id = 2after parallel region 1 thread id = 0parallel region 2 thread id = 0parallel region 2 thread id = 2parallel region 2 thread id = 3parallel region 2 thread id = 1after parallel region 2 thread id = 0parallel region 3 thread id = 0parallel region 3 thread id = 1parallel region 3 thread id = 3parallel region 3 thread id = 2after parallel region 3 thread id = 0从上面的输出我们可以了解到，id = 0 的线程就是主线程，在并行域内部程序的输出是没有顺序的，但是在并行域的外部是有序的，在并行域的开始部分程序会进行并发操作，但是在并行域的最后会有一个隐藏的同步点，等待所有线程到达这个同步点之后程序才会继续执行，现在再看上文当中 openmp 的执行流图的话就很清晰易懂了。
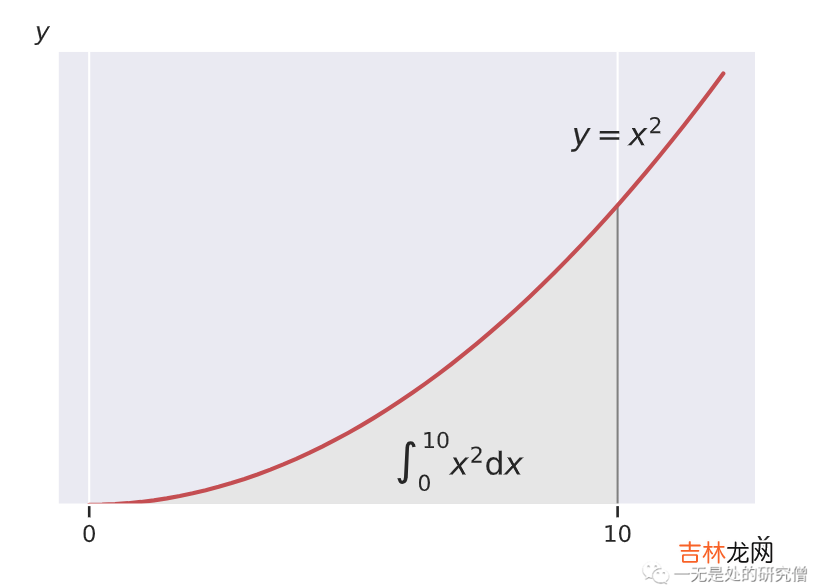
积分例子现在我们使用一个简单的函数积分的例子去具体了解 openmp 在具体的使用场景下的并行。比如我们求函数\(x^2\) 的积分。

文章插图
\[\int_0^{x} x^2 = \frac{1}{3}x^3dx + C\]比如我们现在需要 x = 10 时，\(x^2\) 的积分结果。我们在程序里面使用微元法去计算函数的微分结果，而不是直接使用公式进行计算，微元法对应的计算方式如下所示：
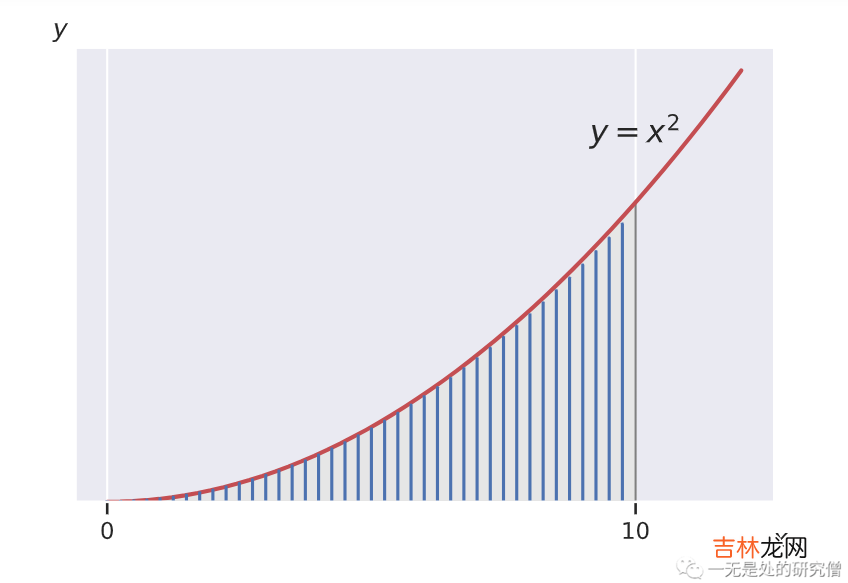
\[\int_0^{10} x^2\mathrm{d}x =\sum_{ i= 0}^{1000000}(i * 0.00001) ^2 * 0.00001\]微元法的本质就是将曲线下方的面积分割成一个一个的非常小的长方形，然后将所有的长方形的面积累加起来，这样得到最终的结果。

文章插图
如果你不懂上面所谈到的求解方法也没关系，只需要知道我们需要使用 openmp 去计算一个计算量比较大的任务即可。根据上面微元法的公式我们有一个非常大的求和公式，如果是在单线程的情况下我们使用一个循环就可以了，但是现在我们有多个线程，那么我们可以让每个线程求某一个区间的和，最后将各个区间的和加起来得到最终的结果，这就是在并发场景下的实现思路。
openmp 具体的实现代码如下所示：

#include <stdio.h>#include <omp.h>#include <math.h>/// @brief 计算 x^2 一部分的面积/// @param start 线程开始计算的位置/// @param end线程结束计算的位置/// @param delta 长方形的边长/// @return 计算出来的面积double x_square_partial_integral(double start, double end, double delta) {double s = 0;for(double i = start; i < end; i += delta) {s += pow(i, 2) * delta;}return s;}int main() {int s = 0;int e = 10;double sum = 0;#pragma omp parallel num_threads(32) reduction(+:sum){// 根据线程号进行计算区间的分配// omp_get_thread_num() 返回的线程 id 从 0 开始计数 ：0, 1, 2, 3, 4, ..., 31double start = (double)(e - s) / 32 * omp_get_thread_num();double end= (double)(e - s) / 32 * (omp_get_thread_num() + 1);sum = x_square_partial_integral(start, end, 0.0000001);}printf("sum = %lf\n", sum);return 0;}

在上面的代码当中 #pragma omp parallel num_threads(4) 表示启动 4 个线程执行 {} 中的代码，reduction(+:sum) 表示需要对 sum 这个变量进行一个规约操作，当 openmp 中的线程遇到 reduction 子句的时候首先会拷贝一份 sum 作为本地变量，然后在并行域当中使用的就是每一个线程的本地变量，因为有 reduction 的规约操作，因此在每个线程计算完成之后还需要将每个线程本地计算出来的值对操作符 + 进行规约操作，也就是将每个线程计算得到的结果求和，最终将得到的结果赋值给我们在 main 函数当中定义的变量 sum。最终我们打印的变量