MPC：百万富翁问题( 二 ) _生活百科

混淆电路的核心就是“加密电路”设计，这是研究重点和难点，由于任意函数理论上都存在一个等价的电路表示，在计算机中可以使用加法器和乘法器实现，而乘法器/加法器可以通过“与门”、”异或门“等逻辑电路来表示。
下面介绍一种”与门“函数实现加密电路：
假设在安全两方计算中，参与方A和B要计算”与门“的门电路，即两者输入分别是$a,b$，输出是$r=a（and）b$：

下表是“与门”真值表

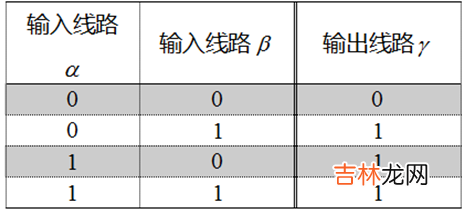
文章插图

第一步，Alice密钥生成：对输入和输出的每个值都生成对应的密钥，在交互过程中使用该密钥替换真实值进行传输，从而避免真实数据的泄露。

文章插图

第二步，Alice进行电路加密（就是替换）：对原始真值表真实的输入和输出数据进行替换得到加密版本：

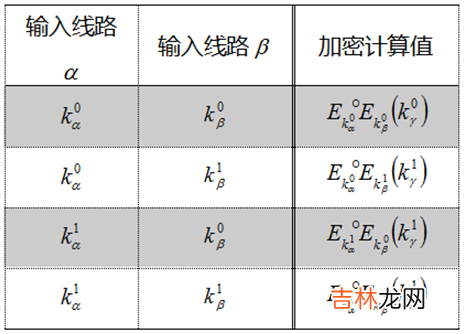
文章插图

第三步，Alice将输出的密文发送给Bob：Alice将第二步得到密文$E_{k_{aj},k_{bi}}(k_{rt})$打乱数据【混淆】之后发送给Bob，同时告知Bob$k_{aj},k_{bi}$的信息，让Bob解密。其中$k_{aj}$对应Alice的输入数据$a$，$k_{bi}$对应于Bob的输入数据，但由于Alice不知道Bob的真实输入数据，便无法确定应该向Bob提供$k_{b0}$还是$k_{b1}$，这是便可以使用OT，既能保证Bob根据自己的输入数据$b$的编号$i$对应的$k_bi$，又能保证Bob只能获得$k_{b0}$和$k_{b1}$中的一个。
第四步，Bob解密：Bob使用Alice提供的$k_{aj}$和OT协议选出的$k_{bi}$对四个密文解密，其中只有密文是$E_{k_{aj},k_{bi}}(k_{rt})$时才能正确解密，否则得到的是乱码。然后Bob将解密结果发给Alice，Alice得到正确结果$r=0$或者$r=1$，并同步给Bob 。

?：

整个过程，Alice没有告诉Bob关于$k_{aj}$对应的真实值，Bob通过OT得到了$k_{bi}$，也没有泄露信息，所以双方在均未泄漏数据的前提下完成了“与门”计算

SSSS的应用在MPC中，主要是利用其同态特性进行函数计算，下面介绍使用SS构造实现加法和乘法运算：
加法假设某公司的 3 个员工分别为 $P_1, P_{2}, P_{3}$，3 人希望在不泄露自己真实工资的情况下, 计算3人的平均工资。
从本质上来讲, 这个问题可以抽象为多方之间的求和问题，我们在此介绍一下使用秘密分享进行求和的思想。
假设员工$P_{1}, P_{2}, P_{3}$ 的工资分别为$x, y, z$，为了计算$r=(x+y+z) / 3$，可以采取以下两个步骤：

秘密分享阶段。每个员工将自己的输入信息 (即工资) 切分成3份, 并分发给另外两个同事; 在分发完成之后, 员工$ P_{i}$ 拥有 3 个值, 分别为$x_{i}, y_{i}, z_{i}$ 。
秘密重构阶段。每个员工分别在本地计算 $ r_{i}=\left(x_{i}+y_{i}+z_{i}\right) / 3$，最终三个员工再将自己的结果 $r_{i} $进行公开, 3 人的平均工资则为 $ r=r_{1}+r_{2}+r_{3}$。

在以上两个步骤中, 每个员工都只得到了同事工资的部分信息, 并不能恢复其真实工资。另外, 根据最终公布的结果$ r_{i}$ 也无法直接推断出$x_{i}, y_{i}, z_{i}$ 三个碎片信息。因此，该方法便使用秘密分享的思想，在保护了各个参与方输入信息的前提下完成均值计算。
乘法假设员工$P_{1}, P_{2}, P_{3}$ 的工资分别为$x, y, z$，为了计算$r=xyz$。
而对于乘法计算，就比较复杂了，因为乘法会涉及交叉项，例如$xy=(x_1+x_2)(y_1+y_2)=x_1y_1+x_1y_2+x_2y_1+x_1y_2$，其中直接计算$x_1y_2,x_2y_1$是非常麻烦的【因为信息属于两个人】，这时就需要引入一些辅助信息：