Unrated, Online Mirror, ICPC Rules, Teams Preferred 2021-2022 ICPC, NERC, Northern Eurasia Onsite J. Job Lookup _生活百科

题意【Unrated, Online Mirror, ICPC Rules, Teams Preferred 2021-2022 ICPC, NERC, Northern Eurasia OnsiteJ. Job Lookup】n个节点，n<=200，你需要构造这n个几点成为一棵树，并且这棵树的中序遍历为1-n;你构造树的节点之间的最短路构成一个n×n的最短距离矩阵d；同时给你n×n的权重矩阵c；最最小的Σdij*cij
思路1. 显然，中序遍历，对于根节点来说，左边的序号小于根，右边的需要大于根2. cij同化成对于i，j之间的最短路上，每条边增加cij，这样相当于对每条边考虑了3. 下面就是常规套路了，区间dp，dp[l][r]代表范围l-r构成的子树，求和的最小值

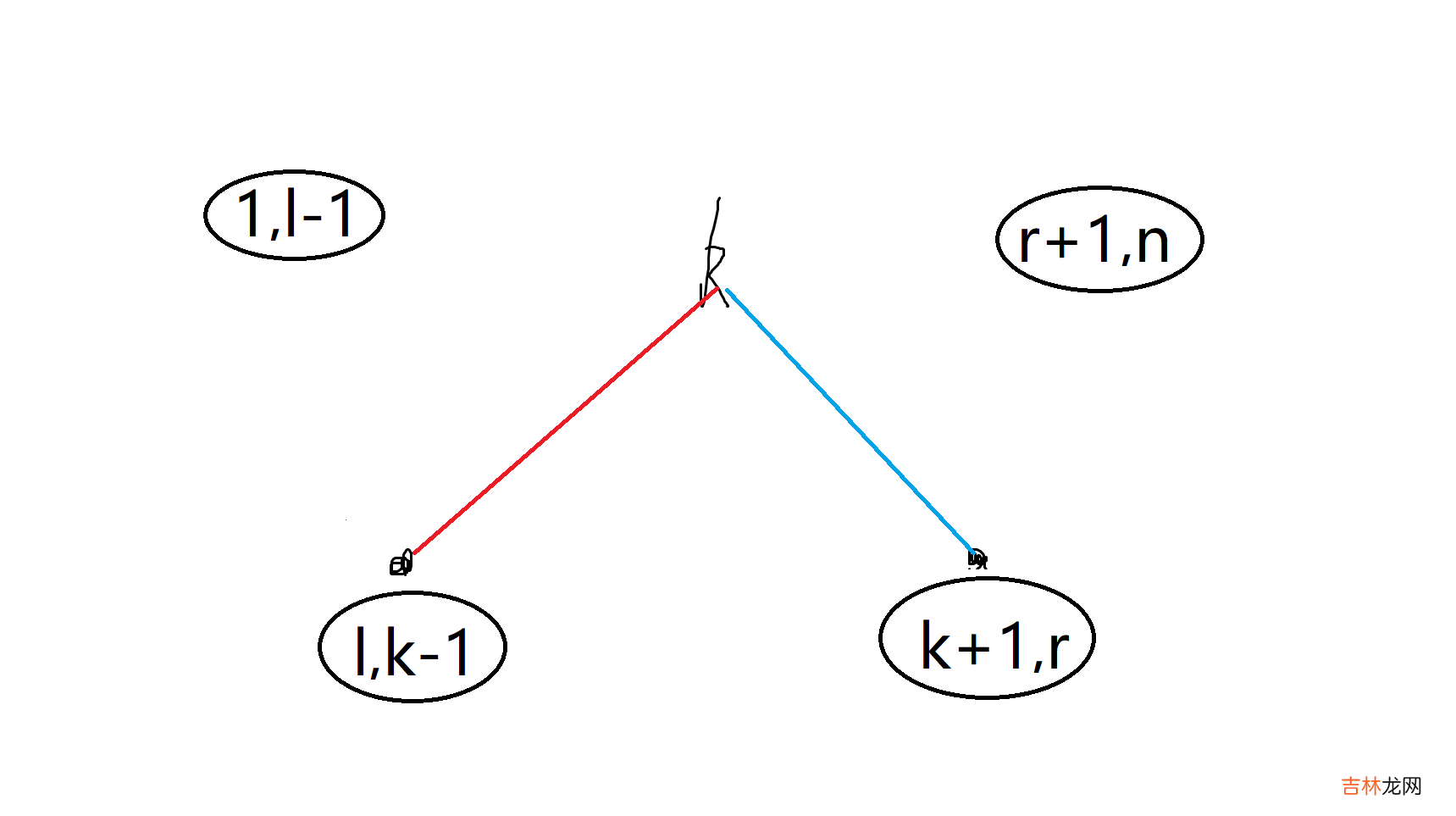
文章插图
枚举l，r的根节点k，显然需要dp[l][r]+=dp[l][k-1]+dp[k+1][r]其次，需要分别统计红色，蓝色线的价值，即左子树内的几点到其他节点，以及右子树内的点到其他节点的价值，这相当与cij的子矩阵求和；这个可以对cij进行前缀和预处理计算得出
代码

#include<bits/stdc++.h>using namespace std;long long a[205][205];long long dp[205][205];int ans[205];int f[205][205];int res(int l, int r) {if (r < l)return 0;int k = f[l][r];ans[res(l, k - 1)] = k;ans[res(k + 1, r)] = k;return k;}long long clc(int l, int r, int ll, int rr) {if (l > r || ll > rr)return 0;return a[r][rr] - a[l - 1][rr] - a[r][ll - 1] + a[l - 1][ll - 1];}int main() {int n;cin >> n;for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {cin >> a[i][j];a[i][j] = (a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + a[i][j]);}}//memset(dp, 0x3f, sizeof dp);//for (int i = 1; i <= n; i++)for (int j = i; j <= n; j++)dp[i][j] = 1e18;//for (int len = 1; len <= n; len++) {//for (int l = 1; l + len - 1 <= n; l++) {//int r = l + len - 1;//for (int k = l; k <= r; k++) {//long long v = dp[l][k - 1] + dp[k + 1][r] ;//v += clc(1, l - 1, l, k - 1) + clc(l, k - 1, k, n);//v += clc(1, k, k + 1, r) + clc(k + 1, r, r + 1, n);//if (v < dp[l][r]) {//dp[l][r] = v;//f[l][r] = k;//}//}//}//}memset(dp, 0x3f, sizeof dp);for (int i = 0; i <= n; i++)dp[i][i] = 0, f[i][i] = i;for (int len = 2; len <= n; len++) {for (int l = 1; l + len - 1 <= n; l++) {int r = l + len - 1;for (int k = l; k <= r; k++) {//long long v = ((l <= k - 1) ? dp[l][k - 1] : 0 )+ ((k + 1 <= r) ? dp[k + 1][r] : 0);long long v = ((l < k - 1) ? dp[l][k - 1] : 0 )+ ((k + 1 < r) ? dp[k + 1][r] : 0);//if (v != vv) {//cout << l<< ' ' <<k<<' '<< r<<'\n';//cout << dp[l][k - 1] << ' ' << dp[k + 1][r]<<'\n';//}v += clc(1, l - 1, l, k - 1) + clc(l, k - 1, k, n);v += clc(1, k, k + 1, r) + clc(k + 1, r, r + 1, n);if (v <= dp[l][r]) {dp[l][r] = v;f[l][r] = k;}}}}//cout << dp[1][n] << '\n';res(1, n);for (int i = 1; i <= n; i++) {cout << ans[i] << ' ';}return 0;}