什么是无理数,无理数是什么意思 _生活百科

1、无理数是什么意思【什么是无理数,无理数是什么意思】无理数的意思是：10进制下的无限不循环小数。
在教学中，无理数是所有不是有理数字的实教，后者是由整教的比率或分构成的字。无理教，也称为无限不环小数，不能写作两整勃之比，若将它写成小教形式，小数点之后的数字有无限多个，并且不会循环。
无理数集合的表示方法：实数集的表示方法为Q，无理数集相当于实数集中有理数集的补集，所以无理数集合符号为CrQ 。
无理数在位置教字系统中表示（倾如，以十进制数字或任何其他自然基础表示）不会终止，也不会重复，即不包数字的子序列。例如，数字的十进制表示以3.141592653589793开始，但没有有限数字的数字可以精确地表示n，也不重复。
历史：
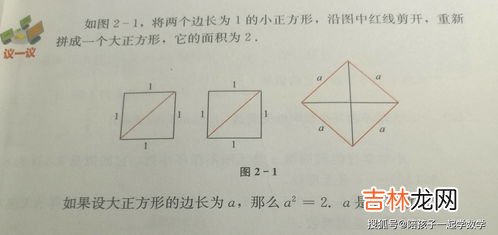
毕达哥拉斯（Pythagoras，约公元前580年至公元前500年间）是古希腊的大数学家。他证明许多重要的定理，包括后来以他的名字命名的毕达哥拉斯定理（勾股定理），即直角三角形两直角边为边长的正方形的面积之和等于以斜边为边长的正方形的面积。
毕达哥拉斯将数学知识运用得纯熟之后，觉得不能只满足于用来算题解题，于是他试着从数学领域扩大到哲学，用数的观点去解释一下世界。经过一番刻苦实践，他提出“万物皆为数”的观点：数的元素就是万物的元素，世界是由数组成的，世界上的一切没有不可以用数来表示的，数本身就是世界的秩序。

文章插图
文章插图
2、什么叫做无理数?无理数指的是无限不循环的数字，数字主要分为有理数和无理数。
在数学中，无理数是所有不是有理数字的实数，后者是由整数的比率构成的数字。
无理数经常是用分数来表示。
常见的无理数有非完全平方数的平方根、π和e等。无理数的另一特征是无限的连分数表达式。
无理数
有理数包括(整数,有限小数,无限循环小数)
无理数指无限不循环小数
特别要注意的是无限循环小数很多人常误以为它属于无理数
等到了高中{有理数}={分数}={循环小数

文章插图
文章插图
3、无理数的概念是什么在数学中，无理数是所有不是有理数字的实数，无理数，也称为无限不循环小数，不能写作两整数之比。
无理数的概念
无理数是指实数范围内不能表示成两个整数之比的数。简单的说，无理数就是10进制下的无限不循环小数，常见的无理数有：圆周长与其直径的比值，欧拉数e ，黄金比例φ等等。无理数最早由毕达哥拉斯学派弟子希伯索斯发现。
有理数和无理数的区别
（1）性质区别：
有理数是两个整数的比，总能写成整数、有限小数或无限循环小数；无理数不能写成两个整数之比，是无限不循环小数。
（2）结构区别：
有理数是整数和分数的统称；无理数是所有不是有理数的实数。
（3）范围区别：
有理数集是整数集的扩张，在有理数集内，加法、减法、乘法、除法(除数不为零)4种运算均可进行；无理数是指实数范围内不能表示成两个整数之比的数。
无理数集及其他数集的符号
无理数集相当于实数集中有理数集的补集，实数集R，有理数集Q，所以无理数集合符号为CrQ 。
所有正整数组成的集合称为正整数集，记作N*，Z+或N+ 。
所有负整数组成的集合称为负整数集，记作Z- 。