连续不一定可导,为什么连续不一定可导？( 二 ) _生活百科

可导性则是指函数在某一点附近存在切线（导数），即函数在该点的左右导数存在且相等。可导性意味着函数在任意小的邻域内可以用线性近似来近似函数的局部变化。
尽管连续性是可导性的一个必要条件，但可导性还需要更严格的条件。例如，函数在某一点处可能是连续的，但由于存在尖点、锐角、断点等异常形状，导数可能不存在。例如，阶梯函数在每个跳跃点都是连续的，但它在跳跃点处不可导。
因此，连续性是可导性的一个较弱要求，只要求函数在某点处无间断，而可导性则要求函数在该点处具有平滑的变化并存在切线。

文章插图
文章插图
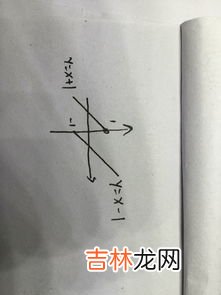
2、可导一定连续,连续不一定可导,这句话对吗,为什么?“可导必连续”，可以导的函数的话，如果确定一点那么就知道之后一点的走向，不会有突变；“连续不一定可导”，连续不可导的话，像尖的顶点，那一个点是不可导的。
可导一定连续，逆否命题同样为真，不连续一定不可导，连续不一定可导。
例如绝对值函数就是连续的，但不可导，可导数一定连续是因为，定义里面就用到了连续的条件。
导数存在和导数连续的区别：
一、满足条件不同
1、导数存在：只要存在左导数或者右导数就叫导数存在。
2、可导：左导数和右导数存在并且左导数和右导数相等才能叫可导。
二、函数连续性不同
1、导数存在：导数存在的函数不一定连续。
2、可导：可导的函数一定连续；连续的函数不一定可导，不连续的函数一定不可导。
三、曲线形状不同
1、导数存在：曲线是不连续的，存在尖点或断点。
2、可导：可导的曲线形状是光滑的，连续的。没有尖点、断点。

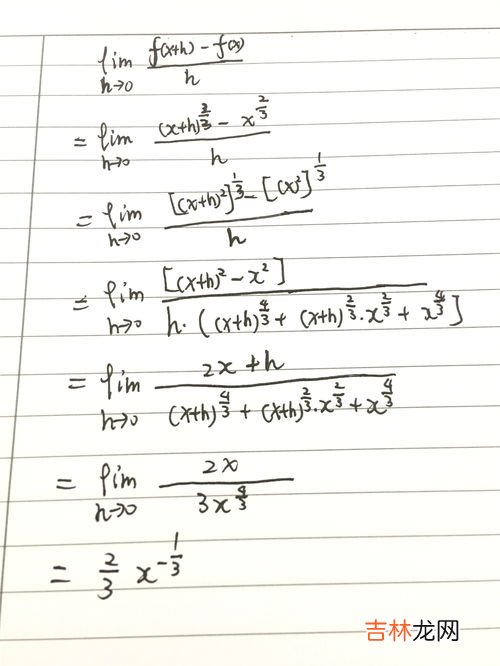
文章插图
文章插图
3、连续函数一定可导吗?函数的条件是在定义域内,必须是连续的.可导函数都是连续的,但是连续函数不一定是可导函数.
也就是说在每一个点上导数的左右极限都相等的函数是可导函数，反之不是。
x1=x2=1 即有2个重复相等的实数根,1就是重根.
k重根—重复相等k次的根,比如上面的实数根1它重复相等了2次,就叫2重根.以此类推
函数f(x)在它的每一个可导点x 。处都对应着一个唯一确定的数值——导数值f′(x)，这个对应关系给出了一个定义在f(x)全体可导点的集合上的新函数，称为函数f(x)的导函数，记为f′(x) 。
导函数的定义表达式为：
值得注意的是，导数是一个数，是指函数f(x)在点x0处导函数的函数值。但通常也可以说导函数为导数，其区别仅在于一个点还是连续的点。
：百度百科-导函数

文章插图
文章插图
4、连续为什么不一定可导?因为如果这个函数前提是连续的设f(x)=|x|这个函数连续，到时在x=0的时候f(x)不可导，这就是连续不一定可导。
在微积分学中,一个实变量函数是可导函数，若其在定义域中每一点导数存在。直观上说，函数图像在其定义域每一点处是相对平滑的，不包含任何尖点、断点。
如果f是在x0处可导的函数，则f一定在x0处连续，特别地，任何可导函数一定在其定义域内每一点都连续。反过来并不一定。事实上，存在一个在其定义域上处处连续函数，但处处不可导。
函数（function）的定义通常分为传统定义和近代定义，函数的两个定义本质是相同的，只是叙述概念的出发点不同，传统定义是从运动变化的观点出发，而近代定义是从集合、映射的观点出发。