旋转抛物面,旋转抛物面怎么画( 二 ) _生活百科

如图a所示，光线Ⅰ和光线Ⅱ分别为两束平行于转轴的入射光，两束入射光的光斑直径均约为1.0mm；G为带毫米刻度的竖直透明屏幕，实验过程中G的刻度面正对着光线Ⅰ及光线Ⅱ（光线Ⅰ及光线Ⅱ近似位于同一平面内）,转轴中心位于G的刻度面内；L为带有毫米刻度的支撑杆；K为水平标尺，其可沿支撑杆上下自由滑动，进而实现对距离的测量。
实验前，借助于专用水平仪，先将实验仪旋转系统的旋转载物平台调节到水平状态。实验测量时，对于某一旋转角速度ω，先等待足够长时间，使旋转抛物液面达到稳定状态，即液面形状不再随时间而变化；然后微调竖直透明屏幕G的方位，使分别平行于转轴入射的光线Ⅰ和光线Ⅱ经抛物液面反射后正好打到透明屏幕G的同一高度位置；
利用水平标尺K和带有毫米刻度的支撑杆L读取两反射光线的交点位置与旋转抛物液面最低点位置之间的距离S ，则S的大小即为当前旋转抛物液面焦距的实验测量值。改变系统的旋转角速度，重复上述的实验过程，即可获取各稳定旋转抛物液面焦距的实验测量值。
稳定旋转液面的凹面焦距与转速之间的定量关系式如上。

文章插图
文章插图
4、什么是旋转抛物面抛物面，是指抛物线旋转180°所得到的面。数学上的抛物线就是同一平面上到定点（焦点）的距离与到定直线（准线）的距离相等的点的集合。
抛物面是二次曲面的一种。抛物面有两种：椭圆抛物面和双曲抛物面。
paraboloid
定义
抛物线旋转180°所得到的面
应用
车灯、手电筒以及雷达
到定点与到定直线距离相等点集合
x^2+y^2-z/a^2=0
抛物面是二次曲面的一种。抛物面有两种：椭圆抛物面和双曲抛物面。椭圆抛物面在笛卡儿坐标系中的方程为：[1]
请点击输入图片描述
双曲抛物面在笛卡儿坐标系中的方程为：
请点击输入图片描述
在车灯、手电筒等照明器具以及雷达中应用得非常多。它们的反光面或者反射面都是抛物面。
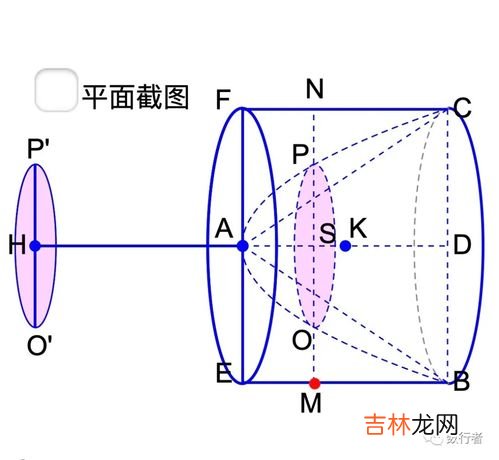
当a = b时，曲面称为旋转抛物面，它可以由抛物线绕着它的轴旋转而成。它是抛物面反射器的形状，把光源放在焦点上，经镜面反射后，会形成一束平行的光线。反过来也成立，一束平行的光线照向镜面后，会聚集在焦点上。[2]
椭圆抛物面的参数方程为：
请点击输入图片描述
高斯曲率为：
请点击输入图片描述
平均曲率为：
请点击输入图片描述
它们都是正数，在顶点处最大，越远离顶点曲率越小，并趋近于零。
双曲抛物面的参数方程为：
请点击输入图片描述
高斯曲率为：
请点击输入图片描述
平均曲率为：
请点击输入图片描述