哈希的误差:哈希只是使得相似的向量落入相同桶的概率更高,为了进一步提高这个概率,可以进行多次不同的哈希函数对输出结果取交际,进一步降低近似带来的信息损失 。也就是用更多的时间和空间来换取更好的近似效果
每个序列哈希分桶的大小可能不尽相同,无法进行batch计算:这里作者又做了一步近似 。根据以上的哈希结果对token进行重排序,相同哈希的token放一起,桶内按原始位置排序,按固定长度m进行切分,每个chunk的query对当前chunk和前一个chunk的key计算注意,也就是位于[m,2m]的query对[0,2m]的key计算注意力,这里m和哈希桶数反向相关\(m=\frac{l}{n_{bucket}}\),也就是和平均哈希桶的大小正相关 。实际上LSH只是用来排序,提高固定长度内注意力权重占整个序列的比例,从而通过有限长度的注意力矩阵近似全序列的注意力结果 。同样是固定窗口,LSH使得该窗口内的token权重会高于以上Longformer,BigBird这类完全基于位置的固定窗口的注意力机制,不过LSH的搜索和排序也会进一步提高时间复杂度
- 可逆残差网络
【Bert不完全手册9. 长文本建模 BigBird & Longformer & Reformer & Performer】可逆残差的概念是来自The reversible residual network: Backpropagation without storing activations(Gomez2017) 。通过引入可逆变换,RevNet使得模型不需要存储中间层的参数计算梯度,每一层的参数可以由下一层通过可逆运算得到 。属于时间换空间的方案,因为反向传播计算梯度时需要先还原本层的参数,因此时间上会增加50%左右~ 细节我们就不多展开想看math的往苏神这看可逆ResNet:极致的暴力美学, 简单易懂的往大师兄这看可逆残差网络RevNet
- 分块计算
分块主要针对FFN层 。因为Feed Forward一般会设置几倍于Attention层的hidden size,通过先升维再降维的操作提高中间层的信息表达能力,优化信息的空间分布,以及抵消Relu带来的信息损失 。但是过大的hidden size会带来极高的空间占用 。因为是在embedding维度进行变换每个位置之间的计算独立,因此可以分块进行计算再拼接,用时间来换空间
效果评测部分我们在下面的performer里一起讨论
Performer
- paper: Rethinking Attention with Performers
- github: https://github.com/google-research/google-research/tree/master/performer
- Take Away: 提出核函数使得QK变换后的内积可以近似注意力矩阵,配合乘法结合律把复杂度从平方降低到线性

文章插图
多头注意力机制的计算是query和key先计算Attention矩阵A,再对V进行加权,也就是上图等号左边的计算顺序,复杂度是序列长度的平方 。为了避免计算\(L^2\)的注意力矩阵,作者采用矩阵分解\(q^{\prime} \in R^{L,r},k^{\prime} \in R^{L,r}\),这里r<d<<L,配合矩阵乘法的结合律,K先和V计算再和Q内积,把空间复杂度从平方级降低到线性 。但是注意力矩阵过softmax之后无法直接做可逆转换得到\(q^{\prime},k^{\prime}\), 因此作者提出了使用positive Random Feature对QK进行映射,使得映射后的矩阵\(q^{\prime},k^{\prime}\)内积可以近似Attention矩阵 。简单解释就是以下的变换
\[softmax(QK^T)V = \phi(Q) \cdot \phi(K)^T \cdot V = \phi(Q) \cdot(\phi(K)^T \cdot V)\]所以Performer的核心在\(\phi\)核函数的设计使得映射后的QK内积可以高度近似注意力矩阵,具体设计如下
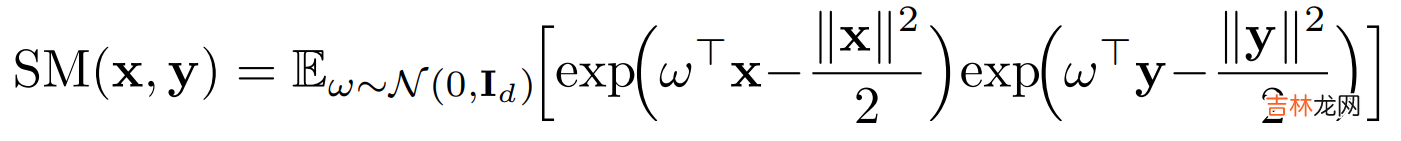
经验总结扩展阅读
-
39奇妙的中医|血糖高了,皮肤会通风报信,尽早察觉3种“怪异”变化,别拖延
-
-
-
-
edg赢了是什么梗,EDG加冕S11总决赛冠军登热搜,网友们讨论的焦点是什么?
-
-
他用君子之交淡如水来形容和约束与她之间的这段感情 为什么有些女人很惧怕爱情?
-
2022年农历十一月廿十宜塑绘吗 2022年12月13日是塑绘吉日吗
-
华为p10屏幕尺寸多大 华为p10屏幕尺寸及参数介绍
-
-
-
-
-
风管风压传感器有哪些功能 风管风压传感器功能特点介绍【详解】
-
暗黑三打造装备怎么能出远古(暗黑3远古靠重铸还是刷大米)
-
粉色|“小作精”虞书欣的私服穿搭,少女感十足超可爱,不愧是活力女孩
-
-
-
都说小白菜地里黄|岳母来家住了一周,他们走后丢了钱包,打开衣柜就说不出话了
-