GLA 论文解读《Label-invariant Augmentation for Semi-Supervised Graph Classification》( 二 ) _生活百科

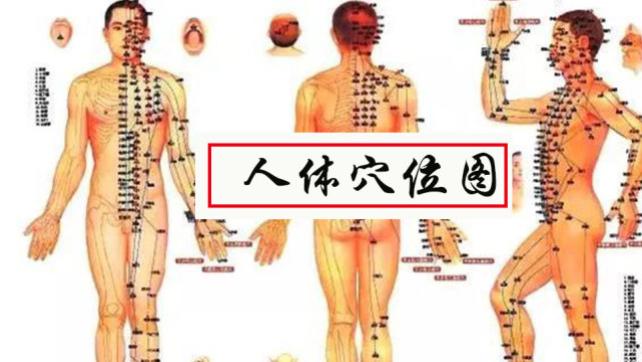
$P^{(l+1)}=\sigma\left(P^{(l)} \cdot \theta_{P}^{(l)}\right) \quad\quad\quad\quad(6)$
采用一个 2 层多层感知器，从原始表示 $H^{O}$ 和增广表示 $H^{A}$ 中得到投影 $P^{O}$ 和 $P^{A}$ 。
2.2.5 Objective Function目标函数包括对比损失和分类损失。对比损失采用 NT-Xent ，但只保留正对部分如下：
$\mathcal{L}_{P}=\frac{-\left(P^{O}\right)^{\top} P^{A}}{\left\|P^{O}\right\|\left\|P^{A}\right\|} \quad\quad\quad\quad(7)$
对于分类损失，采用交叉熵，其定义为：
$\mathcal{L}_{C}=-\sum_{i=1}^{c}\left(Y_{i}^{O} \log P_{i}^{O}+Y_{i}^{O} \log P_{i}^{A}\right) \quad\quad\quad\quad(8)$
其中， $Y^{O}$ 是输入图的标签， $c$ 是图类别的数量。本文只计算带标签的图的 $\mathcal{L}_{C}$ 。$\text{Classifier}$ 的改进将有助于标签不变的增强，反过来有利于分类器的训练。
结合等式 $\text{Eq.7}$ 和 $\text{Eq.8}$ ，总体目标函数可以写成如下：
$\underset{\Theta}{\text{min}} \quad\mathcal{L}_{P}+\alpha \mathcal{L}_{C}\quad\quad\quad\quad(9)$
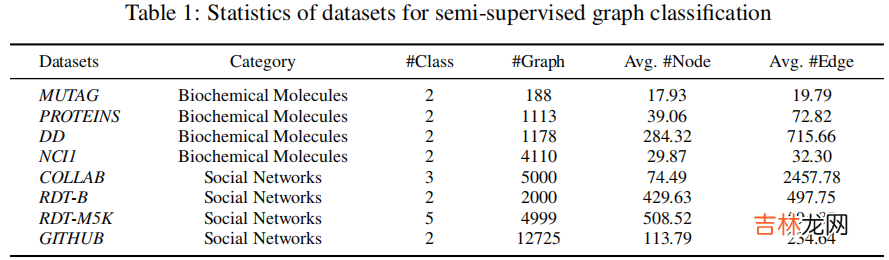
3 Experiments3.1 Datasets

文章插图
3.2 Semi-supervised graph classification results

文章插图
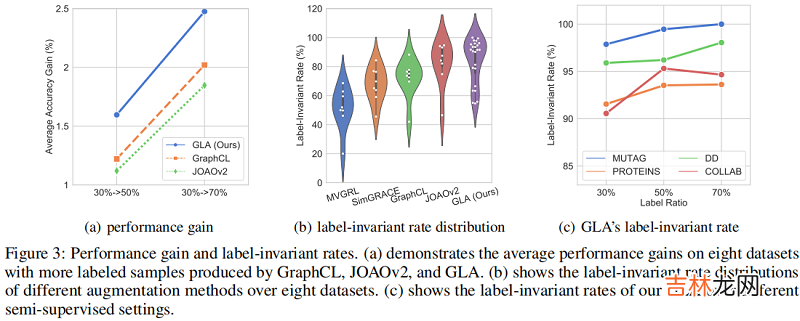
3.3 Algorithmic Performance

文章插图
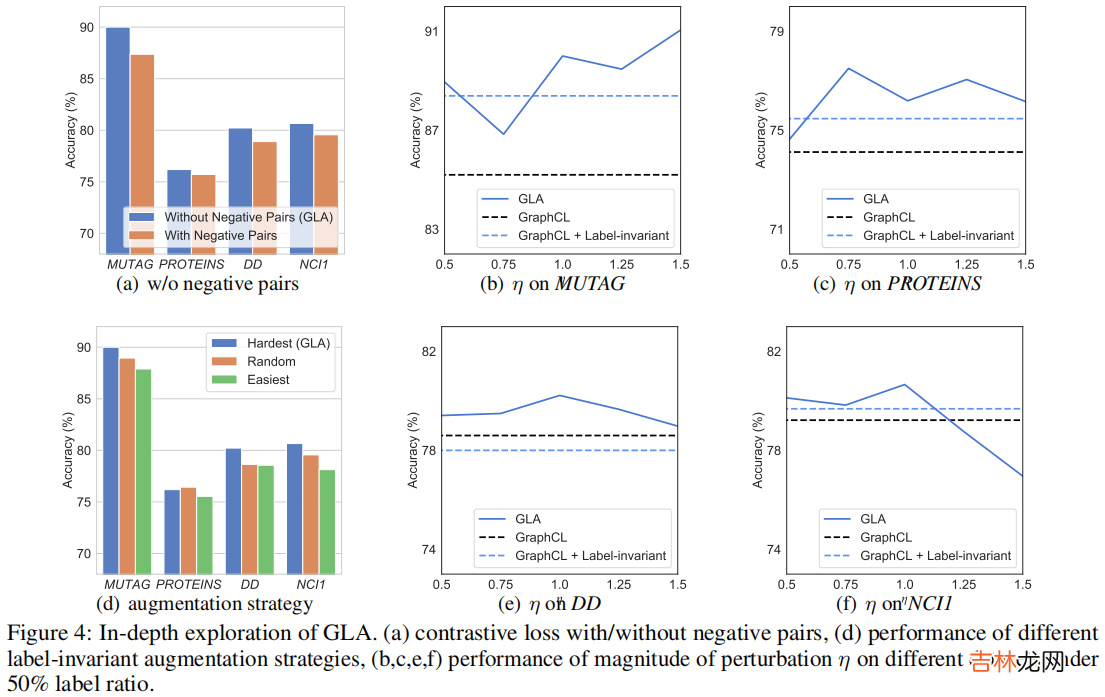
3.4 In-depth ExplorationNegative Pairs现有的图对比学习方法将来自不同源样本的增广图视为负对，并对这些负对采用实例级判别。由于这些方法分离了 pre-train 阶段和 fine-tuning 阶段，因此负对包含了来自不同源样本的增强样本，但在下游任务中具有相同的类别。
Figure 4(a) 显示了我们在四个数据集上有负对和没有负对的 GLA 的性能。可以看到，与没有负对的默认设置相比，有负对的性能显著下降，而负对在所有四个数据集上都表现一致。与现有的图对比方法不同， GLA 集成了预训练阶段和微调阶段，其中以自监督的方式设计的负对不利于下游任务。这一发现也与最近的[10,9]在视觉对比学习领域的研究结果相一致。

文章插图
4 Conclusion本文研究了图的对比学习问题。从现有的方法和训练前的方法不同，我们提出了一种新的图标签不变增强（GLA）算法，该算法集成了训练前和微调阶段，通过扰动在表示空间中进行标签不变增强。具体来说， GLA首先检查增广表示是否服从标签不变属性，并从合格的样本中选择最困难的样本。通过这种方法， GLA在不生成任何原始图的情况下实现了对比增强，也增加了模型的泛化。在8个基准图数据集上的半监督设置下的广泛实验证明了我们的GLA的有效性。此外，我们还提供了额外的实验来验证我们的动机，并深入探讨了GLA在负对、增强空间和策略效应中的影响因素。
【GLA 论文解读《Label-invariant Augmentation for Semi-Supervised Graph Classification》】