GLA 论文解读《Label-invariant Augmentation for Semi-Supervised Graph Classification》 _生活百科

论文信息

论文标题：Label-invariant Augmentation for Semi-Supervised Graph Classification论文作者：Han Yue, Chunhui Zhang, Chuxu Zhang, Hongfu Liu论文来源：2022 ， NeurIPS论文地址：download论文代码：download

1 Introduction我们提出了一种图对比学习的标签不变增强策略，该策略涉及到下游任务中的标签来指导对比增强。值得注意的是，我们不生成任何图形数据。相反，我们在训练阶段直接生成标签一致的表示作为增广图。
2 Methodology2.1 Motivation数据增强在神经网络训练中起着重要的作用。它不仅提高了学习表示的鲁棒性，而且为训练提供了丰富的数据。
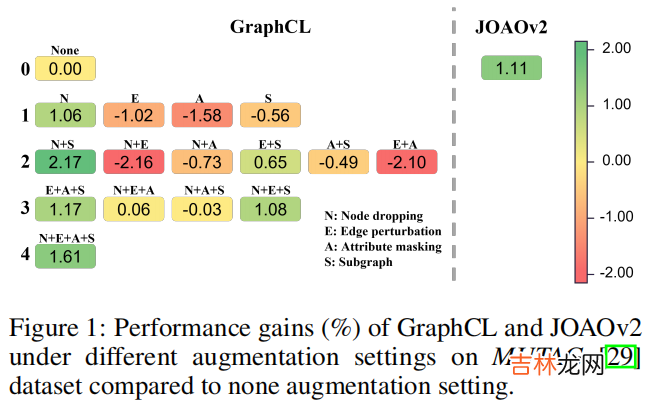
例子：（使用 $50%$ 的标签做监督信息。数据增强：node dropping, edge perturbation, attribute masking, subgraph sampling）

GLA 论文解读《Label-invariant Augmentation for Semi-Supervised Graph Classification》

文章插图
显然有些数据增强策略（或组合）对于模型训练又负面影响。本文进一步使用 MUTAG 中的 $100%$ 标签训练模型，然后以每种数据增强抽样概率 $0.2$ 选择数据增强图，发现 80% 的数据增强图和原始图标签一致，约 $20%$ 的数据增强图和原始图标签不一致。
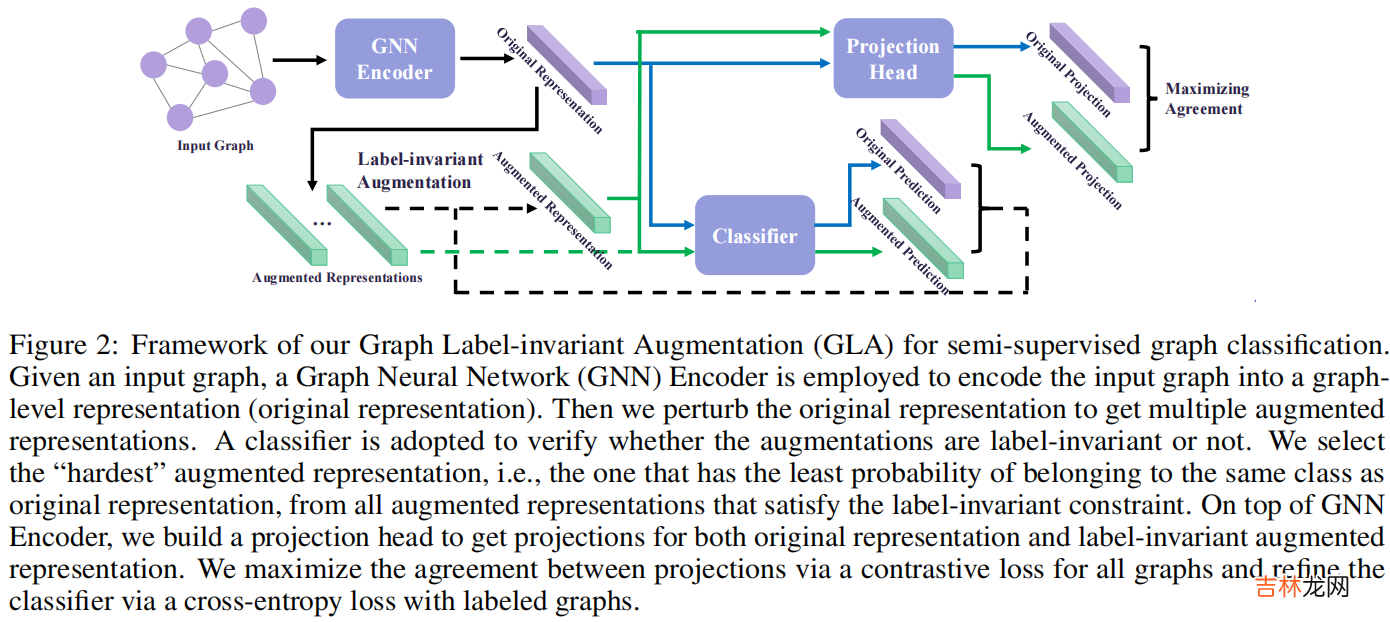
2.2 Label-invariant Augmentation整体框架：

文章插图
四个组成部分：

- Graph Neural Network Encoder
- Classifier
- Label-invariant Augmentation
- Projection Head

出发点：对于一个有标记的图，我们期望由增强表示预测的标签与地面真实标签相同。
2.2.1 Graph Neural Network EncoderGCN layer :
$G^{(l+1)}=\sigma\left(\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}} G^{(l)} \theta_{G}^{(l)}\right)\quad\quad\quad\quad(1)$其中：

- $G^{(l)}$ denotes the matrix in the l -th layer, and $G^{(0)}=X$
- $\sigma(\cdot)=\operatorname{ReLU}(\cdot)$

池化 (sum)：
$H=\operatorname{Pooling}(G)\quad\quad\quad\quad(2)$
2.2.2 Classifier基于图级表示，我们使用带有参数 $\theta_{C}$ 的全连接层进行预测：
$C^{(l+1)}=\operatorname{Softmax}\left(\sigma\left(C^{(l)} \cdot \theta_{C}^{(l)}\right)\right)\quad\quad\quad\quad(3)$
其中， $C^{(l)}$ 表示第 $l$ 层的嵌入，输入层 $C^{(0)}=H^{O}$ 或 $C^{(0)}=H^{A}$ 分别表示原始表示和增强图表示。实验中，采用了一个 2 层多层感知器，得到了对原始表示 $H^{O}$ 和增强表示 $H^{A}$ 的预测 $C^{O}$ 和 $C^{A}$ 。
2.2.3 Label-invariant Augmentation不对图级表示做数据增强，而是在原始图级表示$H^{O}$上做微小扰动得到增强图级表示。
在实验中，首先计算所有图的原始表示的质心，得到每个原始表示与质心之间的欧氏距离的平均值为 $d$ ，即：
$d=\frac{1}{N} \sum_{i=1}^{N}\left\|H_{i}^{O}-\frac{1}{N} \sum_{j=1}^{N} H_{j}^{O}\right\|\quad\quad\quad\quad(4)$
然后计算增强图表示 $H^{A}$：
$H^{A}=H^{O}+\eta d \Delta\quad\quad\quad\quad(5)$
其中 $\eta$ 缩放扰动的大小， $\Delta$ 是一个随机单位向量。
为实现标签不变增强，每次，随机生成多个扰动，并选择符合标签不变属性的合格候选增强。在这些合格的候选对象中，选择了最困难的一个，即最接近分类器的决策边界的一个，以提高模型的泛化能力。
2.2.4 Projection Head使用带有参数 $\theta_{P}$ 的全连接层，从图级表示中得到对比学习的投影，如下所示：