经验总结

  1. 首页 > 生活 > >

4 探究Presto SQL引擎-统计计数( 二 )

生活百科


2.1.2 位图向量的应用有了位图向量 ， 该如何使用呢？假设查询SQL为
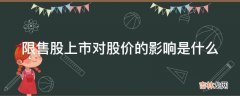
select count(1) from user where age=40;则取age字段位图中age=40的向量：110001 。统计其中1的个数 ， 即可得到最终结果 。
假设查询SQL更复杂一些：
select count(1) from user where age=40 and name='baz'则取age字段位图中age=40的向量：110001和name='foo'的向量：100100 。两个向量进行交集运算：

4 探究Presto SQL引擎-统计计数

文章插图
最后统计结果为1 。
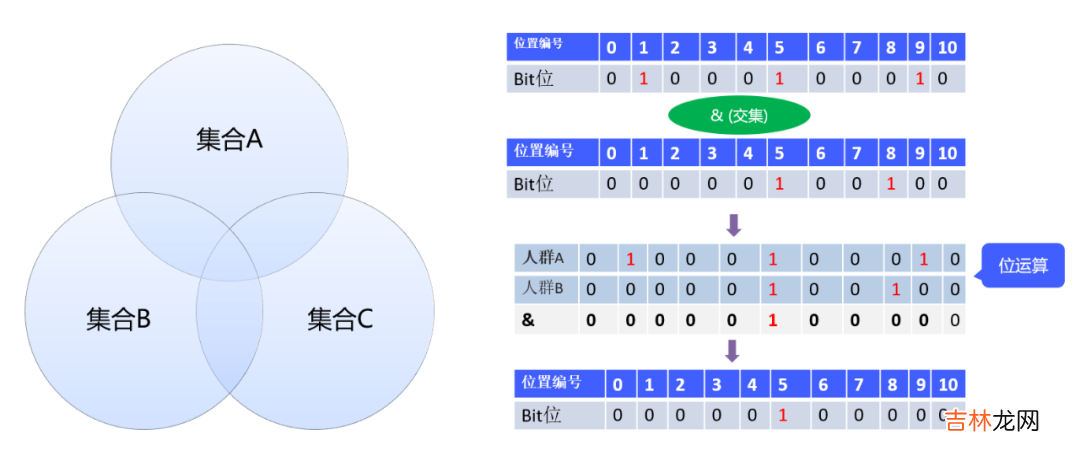
关于Bitmap的思想 ， 笔者认为最巧妙的一点就是通过位运算实现了集合运算 。如下图所示：
4 探究Presto SQL引擎-统计计数

文章插图
在不同的业务场景中 ， 这里的集合可以赋予不同的业务含义 。
2.1.3 位图向量的优点将字段的筛选变成了向量计算后 ， 会非常节约内存 ， 而且可以通过分段长度编码等方式对bitmap向量进行压缩 。而且位运算直接对内存中的二进制位进行操作 ， 执行效率非常高 ， 是性能提升的一大杀器 。
理解了bitmap后 ， 可以发现对于整型字段 ， 可以直接用bitmap进行基数统计 。笔者曾经实验过 ， 对于3亿数据量级使用roaringbitmap工具 ， bitmap消耗内存约30M ， 而且如果数据分布非常密集内存消耗还有很大的压缩空间 。唯一的缺点是非数值型字段 ， 需要进行额外的转换处理 。
2.2 Linear Count算法Linear Count简称LC算法 ， LC算法的流程非常简单(背后的数学思想不简单) 。
算法描述如下：
  • 初始化：给定m个房间 ， 房间存储数字 ， 初始化为0 。
  • 迭代执行：对于要进行基数统计的集合 ， 用一个哈希函数处理集合中的每一个元素 。通过哈希函数处理后 ， 元素就可以放置到一个房间中 。
  • 收尾：统计m个房间中空房间的数量U 。
  • 结论：集合中不重复元素的个数估计值可以通过如下公式计算：n=-m*log(U/m) 。
这样就把一个统计问题转换成了一个数学问题 。公式非常简洁 ， 看到这里大脑中一定会出现许多的问题：
这个公式是怎么得到的？
这里涉及到概率论与数理统计知识 ， 简单来说就是分布、期望、方差、最大似然估计 。数学相关的知识比较初级 ， 陈希孺的《概率论与数理统计》基本能覆盖这个公式的数学原理 。
这个算法的精确度怎么样？
这个问题从数学的角度 ， 就是问方差(标准差) 。这里没法给一个具体的值 ， 跟满桶率控制 ，  m的选择有关 。
这个算法相比精确计数很省空间吗？
这个毋庸置疑 ， 不然直接精确统计就可以了 。
m和最终结果n需要满足什么关系？
（毕竟当没有空房间时 ， 这个公式就有问题了 。） 这里直接给结论吧 ， 随着m和n的增大 ， m大约为n的十分之一 。
2.3 HyperLogLog算法HyperLogLog简称HLL算法 ， 它有如下的特点：
  1. 可以实现由极小的内存开销统计出巨量的数据 。在 Redis中实现的HyperLogLog ， 只需要12K内存就能统计2^64个数据 。
  2. 可以方便实现分布式扩展 。(这个点对算法在业务系统中落地非常关键)
理解HLL算法 ， 需要如下几个知识点的铺垫：伯努利实验、调和平均数 。

经验总结扩展阅读


上一篇：长春市哪个寺庙香火最旺 长春十大著名寺庙排行榜

下一篇：哪些情况会导致征信异常