4 探究Presto SQL引擎-统计计数( 三 ) _生活百科

伯努利实验有很多的呈现方式，本文例举其中的一种：取一枚硬币，不断抛掷，直到硬币落地结果为正面朝上。这样的执行过程称为一轮实验。从描述可以看出一轮实验完成抛掷硬币的次数是随机的。
一轮实验对应的Java代码实现如下：
private Random random = new Random(); /*** 0代表正面* 1代表反面* 抛掷直到出现正面* @return 抛掷的次数*/ public int tossCoin(){int r,cnt=0;do{r=random.nextInt(2);cnt++;}while (r<1);return cnt; }可以看出，每执行一轮实验就会得到一个数字，代表这轮实验抛掷硬币的次数。例如：
执行了10轮，可能的结果如下：
3,1,4,1,1,2,3,4,1,1执行了100轮，可能的结果如下：
1,1,2,1,1,2,1,4,2,1,3,1,1,1,1,3,1,2,1,1,2,4,2,3,2,1,1,1,3,1,2,2,6,1,2,4,1,2,2,1,1,3,1,1,1,1,1,1,1,1,1,4,2,1,1,1,1,1,3,1,2,4,4,4,1,3,2,1,5,1,1,1,1,1,1,1,5,1,1,7,1,1,4,1,3,2,1,1,5,2,1,1,5,2,1,1,4,1,1,1执行了1000轮，可能的结果如下：
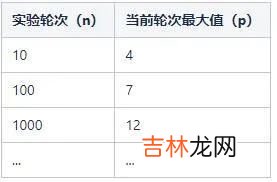
1,2,1,2,1,3,3,3,1,1,2,2,1,2,1,1,1,1,1,2,1,7,1,1,1,2,2,1,1,3,5,2,3,2,3,1,1,3,1,...,4,1,1,1,2,2,1,3,1,1,1,2,1,1,1,2,1,4,2,2,1,2,2,2,1,1,1,2,2,2,1,1,1,2,2,1,1,3,2,6,1,1,1,2,1,1,1,1,1,1,1,2,1,1,1,1,2,1这时候问题就来了，我们这样按上面的规则不停的抛硬币只是为了应付无聊的时间吗？当然不是！我们关注的重点是：

文章插图
当然，这个最大值是随机变动的，它不是一个固定的值。但是隐约中有个规律：执行的轮次越多，轮次对应的最大值也越大。数学上可以给一个很粗略的公式来拟合这种关系：n=2^p 。
换言之，我们可以通过p来估计n 。到这里就出现了问题解决思路的转换：

将基数统计问题转换成概率论里面参数估计的问题。

思维转换到了数学领域，就可以用数学的工具来解决问题。通常用概率论的思维解决问题，会面临如下几个拦路虎。
问题一：最大值不稳定，容易受到极值影响。
在概率上，对于极值我们的处理策略是多实验几轮，通过平均值来消除极值的影响。这个就引出了第二基础知识点：调和平均数。
数学上其实有许多的平均数计算方式：算术平均数、几何平均数、平方平均数。这里选用调和平均数主要是消除极值的影响。通常有个笑话说，我的收入是1万，老板的收入是1亿，我们平均收入是5000万，我被平均了。如果用调和平均数，得到的结果就是1999.98 。
关于调和平均数的公式，非常容易理解：

文章插图
关于数学，确切地说是概率论的知识点，还有很多。例如估计方法是有偏估计还是无偏估计？，估计的方差和标准差是多大？这里涉及到较为底层的概率论知识，就先略过。
略过数学知识，关键的问题在于，我们如何将待基数统计问题跟上面的伯努利实验建立联系？这两个点之间的桥梁就是Hash函数。第一次见识到Hash函数还能这样用，确实大开眼界。